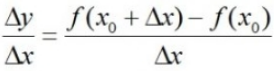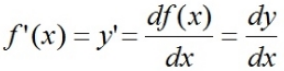Persamaan diferensial merupakan konsep fundamental dalam matematika yang digunakan untuk memodelkan berbagai fenomena dalam berbagai bidang ilmu, termasuk fisika, biologi, ekonomi, dan teknik. Dalam artikel ini, kita akan menjelajahi pengertian, jenis-jenis, solusi, dan aplikasi dari persamaan diferensial.
Pengertian Diferensial

Apa itu Diferensial atau disebut juga turunan ? ialah merupakan suatu fungsi lain dari suatu fungsi sebelumnya. Misalnya pada fungsi f menjadi f’ yang memiliki nilai tidak beraturan.
Konsep turunan sebagai bagian utama dari kalkulus telah dipikirkan pada saat yang bersamaan oleh seorang ilmuan yang bernama Sir Isaac Newton (1642 – 1727).
Dalam penggunaan (diferensial) ialah sebagai suatu alat untuk menyelesaikan berbagai masalah dalam sebuah geometri dan mekanika.
Maka dalam kasus ini diferensial juga dapat diartikan sebagai tingkat perubahan suatu fungsi atas adanya perubahan variabel bebas dari fungsinya tersebut.
Misalkan fungsi : ƒ ( x) = y
Maka, dengan y sebagai variabel terikat dan x sebagai variabel bebasnya, artinya nilai y dipengaruhi oleh nilai x.
Maka kesimpulannya diferensial ialah diartikan sebagai tingkat perubahan dari setiap variabel y sebagai tanggapan terhadap suatu perubahan dalam variabel x.
Di dalam sebuah kasus ekonomi dapat dicontohkan sebagai berikut:
- Misalkan pada sebuah fungsi permintaan, hubungan antara jumlah barang yang diminta dengan tingkat harga. Adanya perubahan tingkat suatu harga pada suatu titik tertentu akan mempengaruhi jumlah barang yang diminta. Maka, pada setiap kasus dan setiap titik bisa sama ataupun berbeda, bergantung terhadap jenis fungsi permintaannya itu sendiri.
- Contoh lainnya dari suatu fungsi kegunaan atas segelas air.
Diferensial (turunan) fungsi dapat dinotasikan sebagai berikut:
Misalnya, ada beberapa fungsi sebagai berikut:
- f (x) =3x + 5
- y = x² – x + 1
- q = 2p² – x + 7
- C = 10 – 5q + 2q²
Jadi, turunan dari fungsi-fungsi di atas dapat dituliskan sebagai berikut:
Persamaan Diferensial
Dalam ilmu matematika persamaan ini berfungsi untuk suatu fungsi satu variabel atau lebih, yang menghubungkan nilai fungsi itu sendiri dan turunnya dalam berbagai orde.
Dalam diferensial mempunyai peranan penting di dalam rekayasa, fisika, ilmu ekonomi dan berbagai macam disiplin ilmu lainnya.
Kemudian untuk gambaran aliran udara didalam saluran dimodelkan sesuai persamaan Navier Stokes.Persamaan diferensial ini muncul didalam berbagai macam bidang sains dan teknologi,
Persamaan diferensial muncul dalam berbagai bidang sains dan teknologi, bilamana hubungan deterministik yang melibatkan besaran yang berubah secara kontinu (dimodelkan oleh fungsi matematika) dan laju perubahannya (dinyatakan sebagai turunan) diketahui atau dipostulatkan.
Maka dalam hal inipada mekanika klasik akan terlihat, di mana gerakan sebuah benda diberikan oleh posisi dan kecepatannya terhadap waktu.
Hukum Newton memungkinkan kita untuk mengetahui hubungan posisi, kecepatan, percepatan dan berbagaia gaya yang bertindak terhadap suatu benda tersebut, dan menyatakannya sebagai persamaan diferensial posisi sebagai fungsi waktu.
Maka dari banyaknya kasus persamaan ini bisa diselesaikan dengan cara eksplisit, dan menghasilkan hukum gerak.
Persamaan diferensial dalam kehidupan sehari-hari ialah guna penentukan sebuah kecepatan bola yang jatuh bebas di udara, hanya dengan memperhitungkan gravitasinya dan tahanan udara.
Kemudian pada percepatan bola yang menuju ke arah tanah ialah merupakan suatu percepatan oleh sebab gravitasi dikurangi dengan perlambatan karena gesekan udara.
Rumus Dan Aturan Diferensial
- Turunan pada fungsi konstan/konstanta
f(x) = k dengan k sama dengan konstanta, maka f'(x) = 0
- Turunan pada fungsi x berpangkat n
f (x) = xn dengan n = sembarang bilangan, maka f (x) = nxn-1
- Turunan pada fungsi dengan koefisien c.
f (x) = cxn…jadi f (x) = cn.xn-1
- Aturan penjumlahan dan pengurangan fungsi dalam suatu turunan.
f (x) = g(x) ± h(x) jadi f (x) = g (x) ± h(x)
- Aturan perkalian fungsi dalam suatu turunan
f (x) = g(x),h(x) jadi f (x) = g (x) ,h(x) + g (x) ,h(x)
- Aturan pembagian fungsi suatu turunan
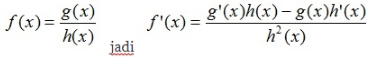
- Aturan rantai dalam suatu turunan
f (x) = g(h(x)) jadi f (x) = g(h(x))h(x)
Difernsial Biasa
Persamaan diferensial biasa lebih mudah dipahami dan diselasaikan dibandingkan persamaan diferensial parsial, yakni persamaan relasi fungsi dengan lebih dari satu variabel.
Dibawah ini ialah beberapa contoh persamaan diferensial biasa.
dibawah ini terdapat beberapa contoh persamaan diferensial parsial
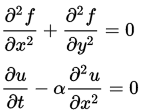
Menentukan Orde
Untuk dapat menentukan orde persamaan diferensial dari turunan tertinggi di dalamnya. Persamaan pertama di dalam contoh di atas ialah persamaan orde pertama.
Persamaan kedua ialah persamaan orde kedua. Derajat dari sebuah persamaan ialah angka pangkat pada suku dengan turunan tertinggi.
- Misalnya, persamaan di bawah ini ialah persamaan orde ketiga, derajat kedua.
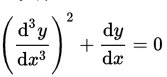
Kita menyebut sebuah persamaan diferensial adalah persamaan diferensial linier apabila derajat dan orde dari fungsi dan semua turunannya bernilai 1.
Jika tidak, persamaan tersebut ialah sebuah persamaan diferensial nonlinier. Persamaan diferensial linier harus mendapat perhatian khusus karena solusinya dapat dijumlahkan dalam kombinasi linier untuk membentuk solusinya berikutnya.
- Di bawah ini terdapat beberapa contoh persamaan diferensial linier.
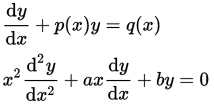
Jenis-Jenis Persamaan Diferensial
Terdapat beberapa jenis persamaan diferensial berdasarkan karakteristik dan bentuknya:
- Persamaan Diferensial Biasa (Ordinary Differential Equations, ODEs): Persamaan ini melibatkan fungsi satu variabel independen. Contoh sederhana adalah persamaan diferensial linier biasa:
����+�(�)�=�(�)dxdy+P(x)y=Q(x)
- Persamaan Diferensial Parsial (Partial Differential Equations, PDEs): Persamaan ini melibatkan fungsi beberapa variabel independen. Contoh PDE adalah persamaan panas:
∂�∂�=�∂2�∂�2∂t∂u=k∂x2∂2u
- Persamaan Diferensial Linier: Persamaan diferensial linier adalah persamaan di mana fungsi yang tidak diketahui dan semua turunannya memiliki pangkat maksimal 1. Contoh ODE linier adalah persamaan diferensial linier homogen:
�2���2+2����+3�=0dx2d2y+2dxdy+3y=0
- Persamaan Diferensial Non-Linier: Persamaan ini melibatkan produk atau pangkat dari fungsi dan/atau turunannya. Contoh ODE non-linier adalah persamaan Lotka-Volterra yang digunakan dalam model hubungan predator-mangsa.
- Persamaan Diferensial Bernoulli: Persamaan ini dapat diubah menjadi persamaan linier melalui substitusi yang sesuai. Contoh:
����−��=�2dxdy−xy=y2
- Persamaan Diferensial Euler: Persamaan diferensial ini memiliki bentuk khusus yang dapat diubah menjadi persamaan aljabar melalui substitusi. Contoh:
�2�2���2+3�����−�=0x2dx2d2y+3xdxdy−y=0
- Persamaan Diferensial Homogen: Persamaan ini hanya mengandung turunan-turunan fungsi yang tidak diketahui, tanpa adanya fungsi asli. Contoh ODE homogen:
�2���2−4�=0dx2d2y−4y=0
- Persamaan Diferensial Tak Homogen: Persamaan ini juga melibatkan fungsi asli selain turunan-turannya. Contoh ODE tak homogen:
�2���2−4�=��dx2d2y−4y=ex
- Persamaan Diferensial Linear Parsial: Persamaan ini adalah jenis PDE di mana setiap suku memiliki turunan-turunan fungsi yang tidak diketahui dalam bentuk linier. Contoh:
∂�∂�+�∂�∂�=�∂2�∂�2∂t∂u+a∂x∂u=b∂x2∂2u
- Persamaan Diferensial Non-Linier Parsial: Persamaan ini melibatkan produk atau pangkat fungsi dan/atau turunannya dalam bentuk PDE. Contoh adalah persamaan Burgers yang muncul dalam dinamika fluida.
Setiap jenis persamaan diferensial memiliki sifat dan metode penyelesaian yang berbeda-beda. Memahami perbedaan antara jenis-jenis ini penting untuk memilih pendekatan yang tepat dalam menyelesaikan persamaan diferensial tertentu sesuai dengan konteksnya.
Solusi Persamaan Diferensial
Solusi dari persamaan diferensial adalah fungsi atau kumpulan fungsi yang memenuhi persamaan tersebut. Solusi dapat dibagi menjadi dua tipe:
- Solusi Umum: Solusi yang mengandung semua solusi khusus dari persamaan diferensial, termasuk parameter-parameter yang belum ditentukan.
- Solusi Khusus: Solusi yang diperoleh dari solusi umum dengan memberikan nilai spesifik pada parameter.
Aplikasi Persamaan Diferensial
Persamaan diferensial memiliki banyak aplikasi penting dalam berbagai bidang ilmu:
- Fisika: Persamaan diferensial digunakan untuk memodelkan fenomena fisika seperti gerak benda, medan elektromagnetik, dan dinamika fluida.
- Biologi: Dalam biologi, persamaan diferensial digunakan untuk menggambarkan pertumbuhan populasi, penyebaran penyakit, dan dinamika ekosistem.
- Ekonomi: Persamaan diferensial digunakan dalam ekonomi untuk menganalisis dinamika pasar, pertumbuhan ekonomi, dan model perilaku konsumen.
- Teknik: Dalam rekayasa, persamaan diferensial digunakan untuk merancang dan menganalisis sistem kontrol, sirkuit listrik, dan struktur mekanik.
- Sains Komputer: Persamaan diferensial digunakan dalam simulasi komputer untuk memodelkan berbagai fenomena yang kompleks, seperti simulasi cuaca dan simulasi fisika dalam video game.
Contoh Soal Diferensial
Contoh Soal 1
Diketahui f’(x) ialah turunan dari f(x) = 5x3+ 2x2+ 6x + 10, Tentukan nilai f’(x) ialah….
Pembahasan :
f(x) = 5x3+2x2+ 6x + 10
f’(x) = 15x2+ 4x +5
f’(3) = 15 . 32 +4 . 3 + 5
= 135 + 12 + 5
= 152
Contoh Soal.2
Sebuah turunan pertama dari f(x) = sin3(3x2 – 3) ialah f‘(x) = …
Pembahasan:
f(x) = sin3(3x2– 3)
f’(x) = sin(3-1)(3x2– 3).3.6x.cos (3x2– 3)
= 18x sin2(3x2– 3) cos (3x2– 3)
Demikianlah materi pembahasan kali ini mengenai persamaan diferensial, semoga artikel ini dapat bermanfaat bagi sobat semua.