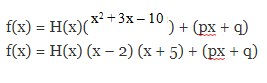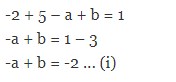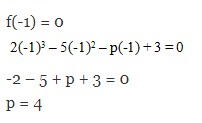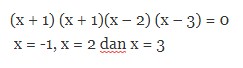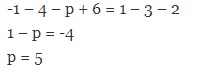Conroh Soal Polinomial – Materi makalah pembahasan kali ini mengenai conth soal polinomial beserta pengertian, bentuk polinomial, nilai polinomial, cara subtitusi, skema horner, teorema sisa teorema faktor dan contoh soalnya, namun dipertemuan sebelumnya kami telah membahas mengenai Contoh Soal Limit Trigonometri. Baiklah langsung aja mari kita simak bersama ulasan dibawah ini.
Pengertian Polinomial
Polinomial atau disebut juga Suku banyak merupakan suatu bentuk suku suku dengan nilai banyak yang disusun dari perubah variabel dan konstanta. Operasi yang digunkana hanya penjumlahan, pengurangan, perkalian dan pangkat bilangan bulat tak negative.
Bentuk Umum Polinomial
Bentuk umum polinomial berderajat n dengan variable x ialah:
| Bentuk Umum | an xn + an-1 xn-1 + . . . + a1 x + a |
| Keterangan | dengan an , an-1 , …. , a1 , a0 € R koefisien/konstanta Polinom an ≠ 0 , dan n merupakan bilangan bulat positif. |
Pangkat tertinggi dari x ialah derajat polinomial, sedangkan suku yang tidak memuat variable (a) dinamakna suku tetap (konstan).
Nilai Polinomial
Nilai polinomial f(x) untuk x=k atau f(k) bisa ditentukan dengan substitusi atau dengan skema Horner
Cara subtitusi |
Dengan mensubtitusikan x = k ke polinomial
f(x) = an kn + an-1 kn-1 + . . . + a1 k + a |
Cara skema horner |
Contoh ; (f(k) = x3 + bx2 + cx + d maka f(k) = ak3 + bk2 + ck + d xa3 + bx2 + cx + d = (ak2 + bk + c)k+d = ((ak + b)k + c)k+d |
Pembagian polinomial
Secara umum dapat dituliskan sebagai berikut :
| Rumus | f(x) = g(x) h(x) + s(x) |
| Keterangan |
|
Pembagian Polinomial Dengan Cara Horner
Pembagian suku banyak f(x) oleh (x-k) dapat dilakukan dengan cara horner.
Teorema sisa dan teorema factor
Bagaimana cara menentukan akar persamaan dengan panmgkat lebih dari dua? Sekarang akan kita pelajari selengkapanya, yaitu dengan menggunakan teorema sisa dan teorema factor.
Teorema sisa
Jika polinom f(x) dibagi x – k maka sisanya ialah f(x).Sifat
Sisa pembagian suku banyak f(x) oleh ax + b ialah
Sisa pembagian suku banyak f(x) oleh (x-a) (x-b) ialah
Teorema faktor
Polinom f(x) mempunyai factor (x-k) apabila dan hanya jika f(x) = 0; k disebut juga akar dari f(x).
Pada Persamaan polinomial mempunyai bentuk an xn + an-1 x n-1 + . . . + a dan (x-k) ialah factor dari f(x), maka nilai k yang mungkin adalah
Cara Horner Bangun Skema Sintentik
Jika kita ingin menentukan suatu nilai polinomial dari f(x)=ax2 + bx +c untuk x = k dengan cara horner, maka dapat disajikan dengan bentuk skema sebagai berikut:
Hitunglah nilai polinomial untuk nilai x yang diberikan berikut ini.
f(x) =x3 + 2×2 +3x -4 untuk x =5
Contoh Soal Polinomial
a. x + 34
b. x – 34
c. x + 10
d. 2x + 20
e. 2x – 20
PEMBAHASAN:Rumusnya adalah P(x) = H(x) . pembagi + (px + q)
Dari soal diketahui:
– f(x) ÷ (x – 2) sisa 24, maka:
f(x) = H(x)(x – 2) + 24
Subtitusikan x = 2, maka:
f(2) = H(2)(2 – 2) + (2p + q)
= 2p + q = 24 …. (i)
– f(x) ÷(x + 5) sisa 10, jadi:
f(x) = H(x)(x + 5) + 10
Dengan Subtitusikan x = -5, jadi:
(f(-5) = H(-5)(-5 + 5) + (-p + q)
= -5p + q = 10 …. (ii)
Eliminasikan persamaan (i) dan (ii):2p +q =24-5p +q =107p = 14p =2
Dalam mensubtitusikan p = 2 pada 2p + q = 24
2(2) + q = 24
q = 24 – 4
q = 20
Jika f(x) dibagimaka:
sisapx + q = 2x + 20
JAWABAN: D
Suku banyak
a. 16x + 8
b. 16x – 8
c. -8x + 16
d. -8x – 16
e. -8x – 24
PEMBAHASAN:Pembaginya adalah: x² – x -2, maka:
= 0
(x – 2) (x + 1) = 0
x = 2 dan x = -1
Ingat rumus: P(x) = H(x) + (px + q), maka sisanya (px + q), maka:
– x = 2
f(2) = 2p + q
24 – 3(2)3 – 5(2)2 + 2 – 6 = 2p + q
16 – 24 – 20 + 2 – 6 = 2p + q
-32 = 2p + q … (i)
– x = -1
f(-1) = -p + q
(-1) – 3(-1)3 – 5(-1)2 + (-1) – 6 = -p + q
1 + 4 – 5 – 1 – 6 = -p + q
-8 = -p + q …(ii)
Eliminasikan persamaan (i) dan (ii):-32 =2p +q-8 =-p +q-24 =3pp = -8
Apabila disubtitusikan p = –p + q = -8
-(-8) + q = -8
q = -16
Maka , sisanya = p + q = -8x – 16
JAWABAN: D
Diketahui
a. -3
b. -1
c. 1
d. 2
e. 5
PEMBAHASAN:
x2 + x – 6 = 0
(x + 3)(x – 2) = 0
x = -3 dan x = 2
Karena h(x) adalah faktor dari g(x), maka:
– g(-3) = 0
2(-3)3 + a(-3)2 + b(-3) + 6 = 0
-54 + 9a – 3b + 6 = 0
9a – 3b = 48 … (i)
– g(2) = 0
2(2)3 + a(2)2 + b(2) + 6 = 0
16 + 4a + 2b + 6 = 0
4a + 2b = – 22
2a + b = – 11 … (ii)
Eliminasikan persamaan (i) dan (ii):
- 9a -3b 48 | x1 | 9a -3b =48
- 2a +b =-11 | x3 | 6a +3b =-33
- 15a =15
- a = 1
JAWABAN: C
Jika f(x) dibagi oleh
a. 22x – 39
b. 12x + 19
c. 12x – 19
d. -12x + 29
e. -22x + 49
PEMBAHASAN:Misalkan sisa pembagiannya S(x) = px+ q
f(x) dibagi oleh x² – 2x atau x(x -2) → x =2 sisanya 2x + 1, maka:
S(2) = 2x + 1
S(2) = 2(2) + 1
S(2) = 5
2p + q = 5 … (i)
f(x) dibagi oleh x2 – 3x atau x(x – 3) –> x = 3 sisanya 5x + 2, maka:
S(3) = 5x + 2
S(3) = 5(3) + 2
S(3) = 17
3p + q = 17 … (ii)
Eliminasikan (i) dan (ii):2p + q =53p +q =17-p = -12p = 12JAWABAN: C
Polinomial
a. -4
b. -2
c. 0
d. 2
e. 4
PEMBAHASAN:– Dibagi (x + 1) sisanya 1
maka ketika x = -1, h(-1) = 1
– Dibagi (x – 2) sisanya 43
maka ketika x = 2, h(2) = 43
16 + 20 + 2a + b = 43
2a + b = 43 – 36
2a + b = 7 …. (ii)
Eliminasikan (i) dan (ii):2a +b =7-a +b =-23a = 9
a =3
Subtitusikan a = 3 dalam 2a + b = 7
2(3) + b = 7
6 + b = 7
b = 1
Jadi a + b = 3 + 1 = 4
JAWABAN: E
Salah satu faktor dari (2x³ -5x² – px =3) ialah (x + 1). Faktor yang lain dari suku banyak tersebut adalah…
a. (x – 2) dan (x – 3)
b. (x + 2) dan (2x – 1)
c. (x + 3) dan (x + 2)
d. (2x + 1) dan (x – 2)
e. (2x – 1) dan (x – 3)
PEMBAHASAN:Yang merupakan faktornya ialah x + 1 –> x = -1
Ada Duapolinomial
a. 17
b. 18
c. 24
d. 27
e. 30
PEMBAHASAN:Misalkan f(x) =
Apabila ÷(x + 1 ) –> x = -1 akan memiliki sisa sama,maka:
f(-1) = g(-1)
-1 -4 – 5 + m = 1 – 3 – 2
-10 + m = -4
m = -4 + 10
m = 6
Maka nilai 2m + 5 = 2(6) + 5 = 17
JAWABAN: A
a. –x – 2
b. x + 2
c. x – 2
d. 2x + 1
e. 4x – 1
PEMBAHASAN:
Misalkan sisanya = ax + b, maka
= (x – 2)(x – 1)
Maka sisanya adalah:
f(1) = 3
a + b = 3 … (i)
f(2) = 4
2a + b = 4 … (ii)
Eliminasikan (i) dan (ii):2a + b =4a +b = 3a =1
Dalam Subtitusi a = 1 pada a + b = 3
1 + b = 3
b = 2
Maka sisanya ialah: ax + b = x + 2
JAWABAN: B
a. 2
b. 3
c. 4
d. 5
e. 6
PEMBAHASAN:x4 -3×3 -3×2 +7x +6 =0
(1 +)(x3 -4×2 +x +6) =0
(x +1)(x+1- x2 – 5x +6) + 0
a. 7
b. 5
c. 3
d. -5
e. -7
PEMBAHASAN:
a. 1
b. 4
c. 9
d. 16
e. 25
PEMBAHASAN:– Dibagi (x – 2) sisa 7, maka:
f(2) = 7
16 + 8a + 8 + 2b + 5 = 7
8a + 2b = -22
4a + b = -11 … (i)
– Dibagi (x + 3) sisanya 182
f(-3) = 182
81 – 27a + 18 – 3b + 5 = 7
-27a – 3b = 78
9a + b = -26 … (ii)
Eliminasikan (i) dan (ii):9a + b =-264a +b = -115a = -15a = -3
Nilai dari : a2 – 4ab + 4b2 = (-3)2 -4(-3)(1)2 =9 +4 =25
JAWABAN: E
Artikel ContohSoal.co.id Lainnya: