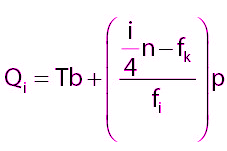Dalam dunia statistik, data merupakan kumpulan informasi atau nilai-nilai yang digunakan untuk menganalisis suatu fenomena atau populasi. Salah satu aspek penting dalam analisis data adalah mengukur seberapa jauh data tersebar. Salah satu metode yang digunakan untuk mengukur persebaran data adalah melalui penghitungan simpangan kuartil. Simpangan kuartil adalah ukuran statistik yang memberikan informasi tentang bagaimana data tersebar di sekitar nilai-nilai kuartil.

Pengertian Simpangan Kuartil

Daftar Isi Tampilkan

Kuartil ialah merupakan suatu nilai-nilai yang membagi data yang telah diurutkan kedalam empat bagian yang nilainya sama besar. Pada saat menentukan letak kuartil data tunggal, Maka harus melihat kondisi jumlah data (n) terlebih dahulu.

Kuartil ialah merupakan suatu bilangan yang dapat dianggap membagi data yang telah diurutkan menurut besarnya, dari yang terkecil keyang terbesar menjadi empat sub kelompok sama banyak.

Jangkauan kuartil disebut juga dengan simpangan kuartil atau rentang semi antar. Kuartil pada suatu data dapat didapatkan dengan cara membagi data tersebut secara terurut menjadi empat bagian yang memiliki nilai sama besar.

K3 – K1. / JAK ialah merupakan jangkauan antar kuartil, K3 dan, K1 =kuartil ke 1).

Nilai Standart (z-Score)

Misalkan kita mempunyai suatu sampel yang berukuran n (banyak datanya = n), dan dari datanya x1, x2, x3,…,xn. Maka rata-rata nya = x. Dan simpangan bakunya ialah s maka membentuk data baru: z1, z2, z3,…, zn dengan menggunakan Koefisien Variasi.

Jenis-Jenis Simpangan Kuartil

Dibawah ini terdapat 3 jenis-jenis kuartil, antara lain:

Kuartil Bawah (Q1)

Langkah awal ialah dengan mencari nilai kuartil bawah, kemudian diperoleh Bb (Batas bawah dari nilai kuartil), fk (frekuensi komulatif) diperoleh dari jumlah frekuensi persis diatas data frekuensi. Lalu fQ1 ialah frekuensi dari data itu tersendiri.

Kuartil Tengah (Q2)

Dengan terlebih dahulu mencari nilai kuartil tengah, lalu diperoleh Bb (Batas bawah dari nilai kuartil), fk (frekuensi komulatif) diperoleh dari jumlah frekuensi persis diatas data frekuensi. Lalu fme adalah frekuensi dari data itu tersendiri.

Kuartil Atas ( Q3)

Dengan terlebih dahulu mencari nilai kuartil atas, lalu diperoleh Bb (Batas bawah dari nilai kuartil), fk (frekuensi komulatif) diperoleh dari jumlah frekuensi persis diatas data frekuensi. Lalu fQ3 adalah frekuensi dari data itu tersendiri.

Rumus Kuartil Untuk Nilai Data Tunggal

Dari keterangan kuartil diatas, maka dapat kita ketahui bahwa kuartil ialah membagi data menjadi empat bagian sama banyak. Oleh sebab itu, terdapat tiga nilai kuartil yang membagi data tersebut.

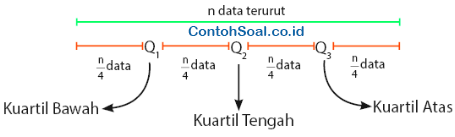
Sebelum melakukan pembagian data, pastikan bahwa data tersebut sebelumnya sudah kita urutkan terlebih dahulu. Untuk lebih jelasnya dapat dilihat ilustrasi dibawah berikut:

Dalam mencari nilai kuartil untuk data tunggal, rumus dibedakan menjadi dua kasus, yakni: untuk jumah data ganjil dan jumlah data genap.

Untuk n ganjil, yakni:

Jenis Kuartil	Rumus Kuarti Data Tunggal
Kuartil Bawah
Kuartil Tengah
Kuartil Atas

Sedangkan cara untuk mencari n genap, yakni:

Kemudian langkah untuk mencari tiga nilai kuartil data tunggal untuk jumlah data genap ialah :

Tentukanlah nilai yang menjadi nilai tengahnya (median atau Q²).
Membagi data di sebelah kiri median menjadi dua bagian yang sama dan menghasilkan kuartil bawah atau Q¹.
Membagi data di sebelah kanan median menjadi dua bagian yang sama dan menghasilkan kuartil atas atau Q².

Rumus Simpangan Kuartil

Di bawah ini merupakan rumus kuartil data kelompok, yaitu:

Rumus

Keterangan :

i = 1 untuk kuartil bawah
i = 2 untuk kuartil tengah
i = 3 untuk kuartil atas
Tb = tepi bawah kelas kuartil
n = jumlah seluruh frekuensi
fk = jumlah frekuensi sebelum kelas kuartil
fi = frekuensi kelas kuartil
p = panjang kelas interval

Cara Menghitung Rumus Kuartil

Cara untuk menentukan kuartil adalah sebagai berikutini .

Urutkan data dari yang terkecil hingga dengan data yang terbesar.
Tentukan Q2 atau median.
Tentukan Q1 dengan cara membagi data di bawah Q2 menjadi dua bagian yang sama besar.
Tentukan Q3 dengan cara membagi data di atas Q2 menjadi dua bagian sama besar.

Contoh Soal Simpangan Kuartil

Contoh Soal 1

Tentukanlah jangkauan interkuartil & simpangan kuartil pada data berikut ini :

Jawaban :

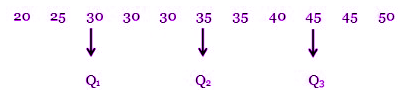
Langkah pertama ialah dengan mengurutkan data untuk mencari kuartil atas & kuartil bawahnya, lihatlah pada gambar dibawah ini.

Jadi, kuartil bawah (Q1) & kuartil atas (Q3), dari kedua data tersebut yakni 30 & 45 maka:

Q_R = Q₃ – Q₁
Q_R = 45 – 30
Q_R = 15

Simpangan kuartilnya yaitu:

Q_d = ½Q_R
Q_d = ½.15
Q_d = 7,5

Jadi jawabannya ialah: jangkauan interkuartil & simpangan kuartil dari data tersebut adalah 15 & 7,5.

Contoh Soal 2

Tentukanlah jangkauan interkuartil & simpangan kuartil pada data berikut ini :

Jawaban:

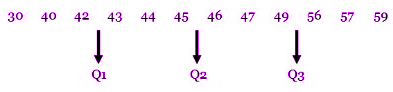
Hal pertama yang harus dilakukan ialah pertama kita akan mengurutkan data untuk mencari kuartil atas & kuartil bawahnya, lihatlah pada gambar dibawah ini.

Jadi :

Q1 = (42 + 43)/2
Q1 = 42,5
Q3 = (49 + 56)/2
Q3 = 52,5

Jadi :

Q_R = Q₃ – Q₁
Q_R = 52,5 – 42,5
Q_R = 10

Simpangan kuartilnya ialah:

Q_d = ½Q_R
Q_d = ½.10
Q_d = 5

Jadi jawabannya ialah: jangkauan interkuartil & simpangan kuartil dari data tersebut ialah 10 & 5.

Kesimpulan

Simpangan kuartil adalah ukuran statistik yang berguna dalam mengukur persebaran data di sekitar kuartil pertama dan kuartil ketiga. Metode ini memberikan gambaran tentang seberapa besar variasi data di dalam “jendela” kuartil, tanpa terlalu dipengaruhi oleh nilai-nilai ekstrem. Meskipun memiliki kelebihan dalam menangani outlier, penting untuk diingat bahwa simpangan kuartil tidak memberikan informasi tentang variasi data di luar rentang kuartil pertama dan kuartil ketiga. Oleh karena itu, dalam analisis yang lebih mendalam, perlu dipertimbangkan juga metode pengukuran lain yang lebih komprehensif.