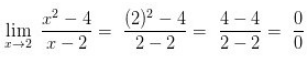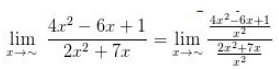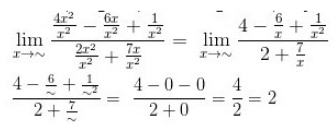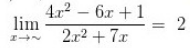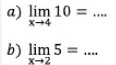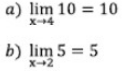Limit Fungsi Aljabar – Setrelah sebelumnya ContohSoal.co.id membahas materi tentang Contoh Soal Limit. Maka dipertemuan kali ini ContohSoal.co.id akan menerangkan secara lengkap materi tentang limit fungsi aljabar beserta penegrtian, materi, metode, rumus dan contoh soalnya.Untuk lebih jelasnya sobat bisa simak ulasan yang sudah ContoSoal.co,id rangkum dibawah ini.
Pengertian Limit Fungsi Aljabar
Limit fungsi aljabar ialah merupakan suatu penentuan nilai fungsi aljabar apabila pada perubahan fungsi tersebut mendekati nilai tertentu.
Ada 2 bentuk dalam menentukan limit fungsi aljabar yakni:
Bentuk pertama
lim f(x)
x→a
lim f(x)
x→a
Bentuk kedua
lim f(x)
x→∼
Rumus Limit Fungsi Aljabar
Dalam matematika, limit umum dituliskan dengan:
| Rumus | lim f(x)=L x→a |
Artinya, apabila x mendekati a tentunya x tidak sama dengan a maka f(x) mendekati L. Pendekatan x ke a dapat dilihat dari dua sisi yakni dari kiri dan kanan atau dengan istilah lain x bisa mendekati dari arah kiri dan kanan sapai menghasilkan limit kiri dan kanan.
Metode Limit Aljabar
Dibawah ini terdapat 4 metode dalam mencari fungsi limit aljabar:
- Metode subitusi
- Metode pemfaktoran
- Metode membagi pangkat tertinggi penyebut
- Metode mengalikan faktor sekawan
Metode Subsitusi
Metode subsitusi yaitu hanya mengganti peubah yang mendekati pada nilai tertentu dengan fungsi aljabarnya
Contoh
lim 3x-1=3(1)-1=3-1=2
x→c
Maka, Nilai funggi limit aljabar yakni
lim 3x -1=2
x→1
Metode Pemfaktoran
Metode pemfaktoran digunakan jika metode subsitusi menghasilkan nilai limit tak terdefinisikan
Contoh :
Metode pemfaktoran dilakukan dengan menentukan faktor persekutuan antara pembilang dan penyebutnya.
Dengan kaitanya pada bentuk limit kedua ada beberapa metode dalam menentukan nilai limit fungsi aljabar yakni metode membagi dengan pangkat tertinggi penyebut dan metode mengalikan dengan faktor sekawan
Metode Membagi Pangkat Tertinggi Penyebut
Contoh :
Tentukan suatu nilai limit fungsi aljabar dibawah ini
Besar pangkat yakni 2, maka
Nilai limit fungsi aljabar tersebut ialah
Metode Mengalikan Dengan Faktor Sekawan
Contoh :
Tentukanlah suatu nilai limit dibawah ini
4-x
lim = . . .
x→4 x-√6x-8
Cara yang utama yang dilakukan untuk menentukan nilai suatu limit yakni dengan mensubtitusikan x = c ke f(x), hingga substitusikan
x=4 ke
Kemudian selanjutnya disubstitusikan dan ternyata nilai limit tidak terdefinisi / merupakan bentuk tak tentu
0
0
Maka itu untuk menentukan nilai limit wajib memakai metode lain. Dan cobalah diperhatikan, pada f (x) terdapat bentuk akar yaitu
√6x -8
Sampai metode perkalian dengan akar sekawaran mampu dilakukan seperti ini.
4-x (4-x)(x+√6x-8)
lim = lim
x→4 x-√6 -8 x→4 x²-√6x-8²
4-x -(x-4)(x+√6x-8)
lim = lim
x→4 x-√6x -8 x→4 x²-√6x-8
Bentuk x² – 6x+8
Difaktotrkan menjadi
Maka, limit fungsi aljabar tersebut yakni-4
Toerema (Pernyataan)
lim f(x) =L jika hanya lim f(x)=L dan lim f(x)=L
x→c x→c¯ x→c+
Pada suatu fungsi dapat dikatakan mempunyai limit apabila antara kiri dan limit kanannya terdapat nilai yang sama dan jika limit kiri dan kanan tidak sama maka nilai limitnya tidak ada.
Sifat Limit Fungsi Aljabar
Apabila n merupakan suatu bilangan bulat positif, k konstanta, f dan g ialah fungsi yang mempunyai limit di c, maka sifat di bawah ini berlaku.
♦. lim k=k
x→c
♦. lim x=c
x→c
♦. lim kf(x)=k lim f(x)
x→c x→c
♦. lim[f(x)+g(x)]=lim f(x)+ lim g(x)
x→c x→c x→c
♦. lim[f(x)- g(x)]=lim f(x)- lim g(x)
x→c x→c x→c
♦. lim[f(x). g(x)]=lim f(x). lim g(x)
x→c x→c x→c
♦. f(x) lim f(x
lim = asalkan lim g(x)≠ 0
x→c g(x) lim g (x) x→c
x→c
♦. lim f(x)]n = [ lim f(x)]n
x→c x→c
♦. lim √f(x) = lim f(x) asalkan lim f(x)>0 bilamana n
x→c x→c x→c
Contoh Soal Fungsi Aljabar
Dibawah ini ialah merupakan sebuah contoh soal agar memudahkan dalam memahami limit fungsi aljabar
Soal No. 1
Tentukanlah nilai fungsi limit dari:
a) lim 10=…
x→4
b) lim 5=..
x→2
Jawab :
Limit bentuk
lim k=k
x→c
di dapat
Demikianlah materi pembahasan kali ini mengenai limit fungsi aljabar, semoga artikel ini dapat bermanfaat bagi sobat semua.
Artikel Lainnya: