Contoh Soal Fungsi Komposisi – Hai para pecinta pelajaran matematika, pada pelajaran kali ini akan membahas tentang makalah materi fungsi komposisi yang meliputi pecahaan, f o g o h, kalkulus, dan lainnya. Akan dibahas juga mulai dari pengertian fungsi koposisi beserta rumus dan contoh soal. Namun dipertemuan sebelumnya kabarkan.com telah membahas mengenai Contoh Soal Barisan Aritmatika, baiklah langsung aja mari kita simak bersama ulasan dibawah ini.
Pengertian Fungsi Komposisi
Fungsi komposisi adalah penyatuan operasi pada dua jenis fungsi f (x) dan (x) untuk menghasilkan fungsi baru Pada komposisi fungsi operasi biasanya dilambangkan dengan “o” dan dibaca dengan komposisi atau bundaran.
Fungsi baru yang dapat terbuat dari fungsi f (x) dan g (x) yaitu:
(f o g)(x) = g dimasukkan ke f
(g o f)(x) = f dimasukkan ke g
Rumus Fungsi Komposisi
Dari rumus tersebut, definisi yang di dapat ialah :
Apabila f=A -> B ditentukan rumus y= f(x),
Apabila g=B -> C ditentukan rumus y= g(x)Jadi, hasil fungsi g dan f :
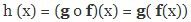
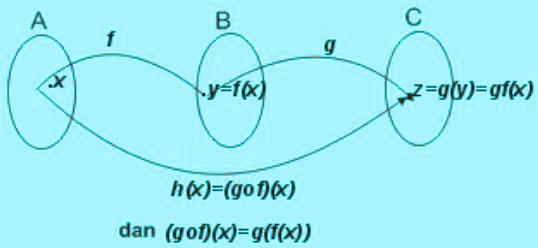
Dari penjelasan tersebut bisa disimpulkan bahwa fungsi yang melibatkan fungsi f dan g bisa ditulis :
(g o f)(x) = g (f(x))
(f o g)(x) = f (g(x))
Berkaitan dengan fungsi komposisi, sebelum anda pelajari contoh soal fungsi komposisi dibawah ini ada baiknya juga Anda pelajari dahulu mengenai fungsi invers.
Fungsi Komposisi pada Kehidupan
Di bawah ini terdapat beberapa contoh fungsi komposisi yang kerap digunakan dalam kehidupan sehari-hari, sebagai berikut:
1. Dalam penysunan sebuah buku dapat dilakuakan dengan menggunakan beberapa proses tahapan, yang diantaranya ialah:
- Fase editorial akan diikuti oleh fase produksi..
- Pada fase editorial, skrip kemudian akan dimodifikasi dan disusun dalam file yang siap untuk dicetak menjadi sebuah buku.
- Proses pembuatan buku ini menggunakan aplikasi dari algoritma fungsi komposisi.
2. Guna melakukan daur ulang logam :
- Pada awalnya, sejumlah potongan logam campuran akan berubah menjadi sejumlah potongan kecil.
- Selanjutnya pada drum magnetik yang terkandung dalam shredder mengesampingkan logam magnetik yang mengandung elemen bes.
- Kemudian sisa potongan logam dikeruk dan kemudian dipisahkan. Sementara itu, serutan besi dilemparkan ke baja baru. Proses daur ulang logam menerapkan fungsi komposisi.
Sifat-sifat Fungsi Komposisi
Di bawah ini terdapat beberapa penjelasan mengenai sifat dari fungsi komposisi, yakni seperti berikut:
Jika f : A → B , g : B → C , h : C → D, jadi dalam hal ini akan berlaku sejumlah sifat contohnya seperti:
- (f o g)(x)≠(g o f)(x). Dalam hal ini tak tidak bersifat komutatif.
- [f o (g o h)(x)] = [(f o g ) o h (x)]. Dalam hal ini memiliki sifat asosiatif.
- Jika fungsi identitas I(x), jadi nantinya akan diberlakukan seperti (f o l)(x)= (lof)(x)= f(x).
Contoh Soal Fungsi Komposisi
Di bawah ini terdapat beberapa contoh soal yang nantinya dapat dijadikan sebagai bahan latihan untuk sahabat semua, simak ulasannya seperti berikut:
Contoh Soal.1Diberikan dua buah fungsi yang masing-masing f (x) dan g (x) berturut-turut yaitu :
f (x) = 3x + 2
g (x) = 2 − x
Tentukanlah:
a) (f o g) (x)
b) (g o f) (x)
Jawaban
Data:
f (x) = 3x + 2
g (x) = 2 − x
a) (f o g)(x)
“Masukkanlah g (x) nya kef (x)”
hingga menjadi:
(f o g)(x) = f ( g(x) )
= f (2 − x)
= 3 (2 − x) + 2
= 6 − 3x + 2
= − 3x + 8
b) (g o f ) (x)
“Masukkanlah f (x) nya ke g (x)”

Hingga menjadi :
= g ( 3x + 2)
= 2 − ( 3x + 2)
= 2 − 3x − 2
= − 3x
Contoh Soal.2Jika Telah diketahui bahwa fungsi dari pada f (x) adalah =3x−1 serta g (x)=2×2+3.
Hasi yang diperoleh dari komposisi ( g o f )(1) =….?
A. 12
B. 8
C. 7
D. 11
E. 9
Jawaban
Dik:
f(x)=3x−1 dan g (x) = 2×2 + 3
( g o f )(1) =…?
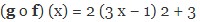
Satukanlah f (x) kedalam g (x) kemudian beri dengan 1
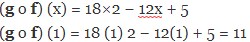
(g o f) (x) = 2 (9 x 2 − 6x + 1) + 3
(g o f) (x) = 18x 2 − 12x + 2 + 3
Contoh Soal.3Diberi dua buah fungsi:
f (x) = 2x − 3
g (x) = x2 + 2x + 3
Apabila (f o g)(a) ialah 33, maka tentukanlah nilai dari 5a
Jawaban:
Cari terlebih dahulu (f o g)(x)
(f o g)(x)=2(x2 + 2x + 3) − 3
(f o g)(x)=2×2 4x + 6 − 3
(f o g)(x)=2×2 4x + 3
33= 2a2 4a= 3
2a2 4a−30 =0
a2+2a−15=0
Kemudian dijadikan faktor:
(a+5)(a−3)=0
a= -5 /a=3
Sampai
5a=5(−5)=−25 atau 5a=5(3)=15
Contoh Soal.4Jika(f o g)(x) = x² + 3x + 4 dan g(x) = 4x – 5. Berapakah nilai dari f(3)?
Jawaban:
(f o g)(x) sama dengan x² + 3x + 4
f (g(x)) sama dengan x² + 3x + 4
g(x) sama dengan 3 Jadi,
4x – 5 sama dengan 3
4x sama dengan 8
x sama dengan 2
f (g(x)) = x² + 3x + 4 dan untuk g(x) sama dengan 3 didapat x sama dengan 2
Hingga : f (3) = 2² + 3 . 2 + 4 = 4 + 6 + 4 = 14
Contoh Soal.5Diketahui g(x) = (x² + 2x – 3)/4. Maka g-’(x) adalah…
Penyelesaian: Agar dapat menemukaan invers yang terdapat di fungsi dalam bentuk kuadrat, maka upaya yang dapat dilakukan yakni dengan cara melakukan perubahan terhadap persamaan umum kuadrat hingga membentuk kuadrat yang sempurna.
Jadi: = x²+2x–3 =x²+2x+1–1–3=(x+1)² – 4
Jadi, g(x) = (x²+2x –3)/4 g(x) = [(x + 1)² – 4]/4
y = [(x + 1)² – 4]/4 4
y = [(x + 1)² – 4] (x + 1)² = 4
y + 4 (x + 1)² = 4(y + 1) x + 1 = √4(y + 1) x + 1 = ±2 √(y + 1) x = -1 ±2 √(y + 1) g-’(x) = -1 ±2 √(x + 1)
Contoh Soal.6Terdapat sebuah dua buah fungsi yang dari masing-masing f(x) dan g(x) secara berturut-turut ialah: f(x) = 3x + 2 g(x) = 2 − x Tentukan: a) (f o g)(x) b) (g o f)(x)
Pembahasan Data: f(x) = 3x + 2 g(x) = 2 − x a) (f o g)(x)
“Masukkan g(x) nya ke f(x)” sehingga: (f o g)(x) = f ( g(x) ) = f (2 − x) = 3(2 − x) + 2 = 6 − 3x + 2 = − 3x + 8 b) (g o f)(x)
“Masukkan f (x) nya ke g (x)” sehingga:
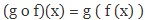
= g ( 3x + 2) = 2 − ( 3x + 2) = 2 − 3x − 2 = − 3x
Contoh Soal.7Selesaikan soal berikut, f(x) = 3×2 + 4x + 1 g(x) = 6x
Tentukan: a) (f o g)(x) b) (f o g)(2)
Pembahasan
Diketahui: f(x) = 3×2 + 4x + 1 g(x) = 6x a) (f o g)(x) = 3(6x)2 + 4(6x) + 1 = 108×2 + 24x + 1 b) (f o g)(2) (f o g)(x) = 108×2 + 24x + 1 (f o g)(2) = 108(2)2 + 24(2) + 1 (f o g)(2) = 432 + 28 + 1 = 461
Contoh Soal.8Diketahui f(x) = x2 + 1 dan g(x) = 2x − 3, maka (f o g)(x) = ….
A. 4×2−12x+10
B. 4×2+12x+10
C. 4×2 − 12x − 10
D. 4×2 + 12x − 10
E. − 4×2 + 12x + 10 (diperoleh dalam soal Ebtanas1989)
Penyelesaiaan:f(x)=x2+1g(x)=2x−3(fog)(x) =…….?
Satukanlah g(x) dengan f(x) (f o g)(x) =(2x − 3)2 + 1 (f o g)(x)= 4×2−12x + 9 + 1 (f o g)(x) = 4×2 − 12x + 10
Contoh Soal.9Apa bila telah diketahui bahwa fungsinya ialah f(x) = 3x − 1 dan g(x) = 2×2 + 3.
Kemudian hitungan dari -pada komposisi fungsi ialah (g o f)(1) =….
A. 7 B. 9 C. 11 D. 14 E. 17
Pembahasan
Diketahui: f(x) = 3x − 1 serta g(x) = 2×2 + 3 (gof)(1) =…….
Masukkan f(x) dengang(x) Lalu beri isi 1
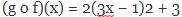
(g o f)(x) = 2(9×2 − 6x + 1) + 3 (g o f)(x) = 18×2 − 12x + 2 + 3
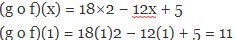
Contoh Soal.10Diberikan dua buah fungsi: f(x) = 2x − 3 g(x) = x2 + 2x + 3
Apabila (f o g)(a) = bernilai 33, maka berapakah nilai dari 5a
Pembahasan Cari (f o g)(x) terlebih dahulu (f o g)(x) = 2(x2 + 2x + 3) − 3 (f o g)(x) = 2×2 4x + 6 − 3 (f o g)(x) = 2×2 4x + 3 33 = 2a2 4a + 3 2a2 4a − 30 = 0 a2 + 2a−15 = 0
Kemudian difaktorkan: (a + 5)(a − 3) = 0 a = − 5 atau a = 3
Maka 5a = 5(−5) = −25 atau 5a = 5(3) = 15
Fungsi komposisi adalah penyatuan operasi pada dua jenis fungsi f (x) dan (x) untuk menghasilkan fungsi baru. Pada komposisi fungsi operasi biasanya dilambangkan dengan “o” dan dibaca dengan komposisi atau bundaran.
Jika f : A → B , g : B → C , h : C → D, jadi dalam hal ini akan berlaku sejumlah sifat contohnya seperti:
(f o g)(x)≠(g o f)(x). Dalam hal ini tak tidak bersifat komutatif.
[f o (g o h)(x)] = [(f o g ) o h (x)]. Dalam hal ini memiliki sifat asosiatif.
Jika fungsi identitas I(x), jadi nantinya akan diberlakukan seperti (f o l)(x)= (lof)(x)= f(x).
Nah demikianlah materi pembahasan mengenai contoh soal fungsi komposisi kali ini, semoga bermanfaat untuk kita bersama.