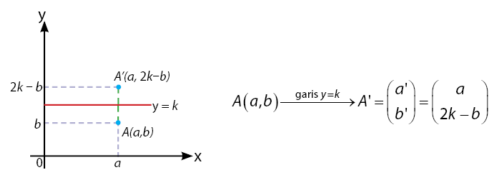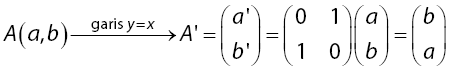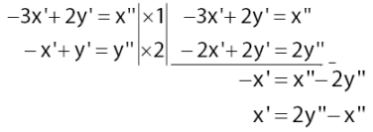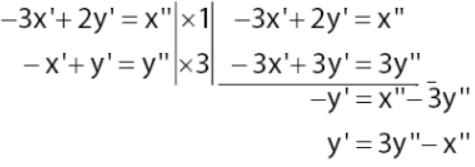Contoh Soal dan Rumus Transformasi Geometri Lengkap

By Posted on

Transformasi Geometri – Setelah sebelumnya ContohSoal.co.id telah membahas materi tentang Integral Subtitusi. Maka dipertemuan kali ini ContohSoal.co.id akan membahas materi tentang transformasi geometri beserta pengertian translasi, rotasi, ditalasi, rumus dan contoh soal. Untuk lebih lengkapnya simak ulasan dibawah ini.

Pengertian Trasformasi Geometri

Daftar Isi Tampilkan

Transformasi Geometri

Apa yang dimaksud dengan Transformasi geometri? ialah  merupakan perubahan suatu bidang geometri yang meliputi posisi, besar dan bentuknya sendiri. Apabila hasil dari transformasi kongruen dengan bangunan yang ditranformasikan, maka dalam hal tersebut  disebut transformasi isometri.

Transformasi isometri sendiri memiliki dua jenisya itu transformasi isometri langsung dan transformasi isometri berhadapan. T

Translasi (Pergeseran)

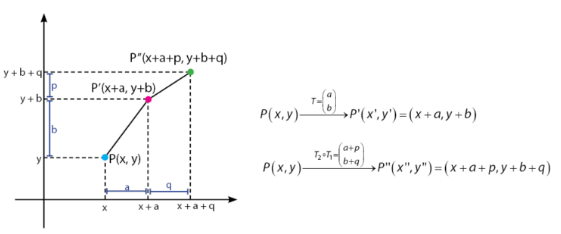
Materi pertama tentang rumus transformasi geometri yang akan dibahas ialah translasi (pergeseran). Translasi merupakan perubahan objek dengan cara menggeser objek dari satu posisi ke posisi lainnya dengan jarak tertentu.

Penentuan hasil objek melalui translasi cukup mudah. Caranya hanya dengan menambahkan absis dan ordinat dengan jarak tertentu sesuai dengan ketentuan. agar lebih lengkap mengenai proses translasi dapat dilihat pada gambar di bawah.

 

Refleksi (Pencerminan)

Selanjutnya ialah refleksi atau yang lebih sering disebut pencerminan. Seperti halnya bayangan benda yang terbentuk dari sebuah cermin.

Sebuah objek yang mengalami refleksi akan memiliki bayangan benda yang dihasilkan oleh sebuah cermin. Namun Hasil dari sebuah  refleksi pada bidang kartesius tergantung sumbu yang menjadi cerminnya.

Pembahasan materi refleksi yang akan diberikan ada tujuh jenis. Jenis-jenis tersebut antara lain adalah refleksi terhadap sumbu x, sumbu y, garis y = x, garis y = -x, titik O (0,0), garis x = h, dan garis y = k.

Baca Juga :  Persamaan Kuadrat Baru - Contoh Soal dan Cara Mencarinya

Berikut ini ialah ringkasan daftar matriks transformasi pada refleksi/pencerminan.

Jenis Pencerminan Matriks
Sumbu x
Sumbu y
Garis y=x
Garis y= -x
Titik 0(0,0)
Garisx = h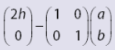
Garis y = k

Berikutnya , simak uraian mengenai matriks transformasi dan setiap jenisnya.

Pencerminan terhadap sumbu x

 

 

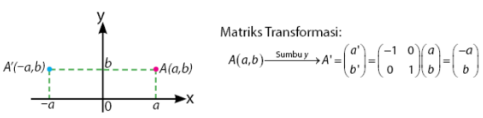
Pencerminan Terhadap Sumbu y

 

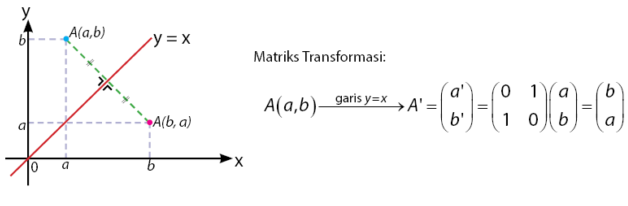
Pencerminan Terhadap Garis y = x

 

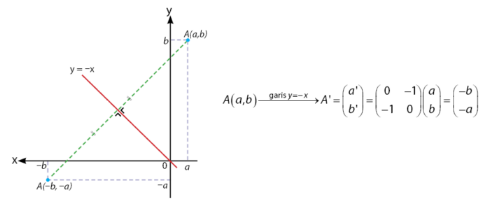
Pencerminan Terhadap Garis y = – x 

 

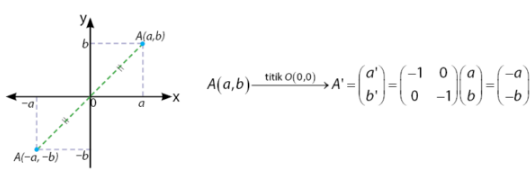
Pencerminan Terhadap Titik Asal O(0,0)

 

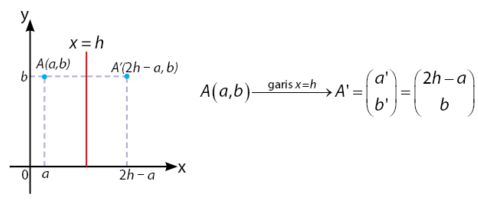
Pencerminan Terhadap Garis x = h

 

Pencerminan Terhadap Garis y = k

Rotasi (Perputaran)

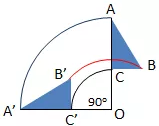
Rotasi atau perputaran merupakan transformasi geometri berupa pergeseran atau pemindahan semua titik pada bidang geometri sepanjang busur lingkaran yang memiliki titik pusat likaran sebagai titik rotasi.

Rotasi dinyatakan positif jika arahnya berlawanan jarum jam, dan bernilai negatif jika searah jarum jam. Sebagai contoh:

 

Titik A berotasi 90o berlawanan arah jarum jam. Dalam diagram cartesius, bentuk-bentuk rotasi sebagai berikut:

Bentuk Rotasi Gambar Rotasi Bentuk Persamaan
Rotasi pada titik 0 (o.0)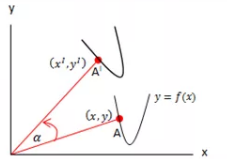
Rotasi pada titik p(a.b)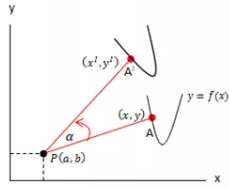

 

Dilatasi

Kemudian apabila pada transformasi translasi, refleksi, dan rotasi hanya dapat mengubah posisi benda, maka dilatasi juga dapat melakukan transformasi geometri dengan merubah ukuran benda.

Ukuran benda dapat menjadi lebih besar atau lebih kecil. Dalam perubahan ini sangat bergantung pada skala yang menjadi faktor pengalinya. Kemudian pada dilatasi terdapat dua rumus, yang dibedakan berdasarkan pusatnya. Berikutnya simak uraian rumus pada transformasi geometri pada dilatasi di bawah.

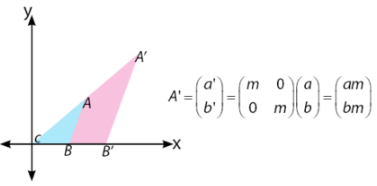
Dilatasi titik A(a,b) terhadap pusat O(0,0) dengan faktor skala m

 

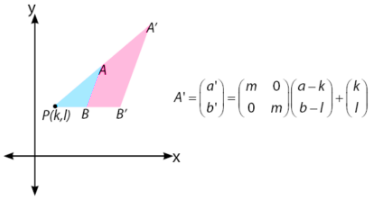
Dilatasi titik  A(a,b) terhadap pusat P(k,l) dengan faktor skala m

 

Contoh Soal Translasi dan Pembahasan

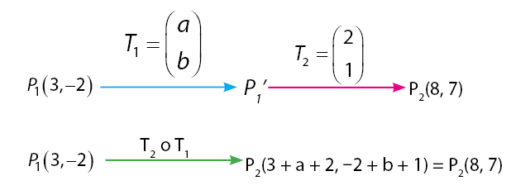
Hasil translasi itik  P¹(3, -2) oleh T¹ dilanjutkan dengan T² = (¹,2) menghasilkan titik .P² (8.7) Komponen translasi dari T¹ yang sesuai ialah ….

A. (83)

B. (38)

C. (35)

D. (18)

E. (15)

Pembahasan:
Misalkan

T1 = (ab)

Diketahui:

T2 = (41)

  Maka

T2. T¹ =

  Perhatikan proses translasi berikut.

Mencari nilai a:

  • 3 + a + 2 = 8
  • a + 5 =8
  • a = 8 – 5 = 3

  Mencari nilai b:

  • – 2 + b 1 = 7
  • b – 1 = 7
  • b = 7 + 1 = 8

Jadi, nilai translasi dari T¹ ialah

T1=(38)

Jawaban: B

Contoh Soal  Transformasi Geometri Refleksi

Persamaan garis  3 x – y – 11 = 0karena refleksi terhadap garis y = x, dilanjutkan oleh transformasi yang bersesuaian dengan matriks ialah ….

  • A.-2x-7y-11=0
  • B.2x+7y-11=0
  • C. – 2x -7y+11=0
  • D.2y-7x+11=o
  • E.2x-7y+11=0
Baca Juga :  Volume Kerucut

Pembahasan:
Pencerminan terhadap garis  y = x ialah:

Berdasarkan rumus di atas, dapat diperoleh kesimpulan bahwa  x¹ = y dan y¹= x . Substitusikan nilai tersebut pada persamaan  3x – y – 11 = 0 sehingga diperoleh persamaan berikut.

  • 3x – y – 11 = 0
  • 3y¹ – x¹ – 11 = 0
  • – x¹ + 3y¹ – 11 = 0

Selanjutnya ialah transformasi yang bersesuaian dengan matriks :

Sehingga, diperoleh dua persamaan berikut.

  • -3x¹ + 2y¹ = x”
  • -x’ + y’ = y”

Mencari nilai x’:

Mencari nilai y’:

Subtitusi hasil x' dan y' di atas pada persamaan  – x’ + 3y’- 11 = 0:

  • -x’+3y’-11=0
  • -(2y”-x”)+3(y”-x”)-11=0
  • -2y”+ x”-9y”-3x”-11=0
  •   -2x”-7y”+11=0
  •   2x”-7y”+11=0

  Jadi, hasil akhir transformasi dari persamaan 3x–y–11=0 ialah 2x–7y+11= 0.

Jawaban: E

 

Demikianlah materi pembahasan kali ini mengenai tranformasi geometri, semoga artikel ini bermanfaat bagi sobat semua.

Artikel Lainnya: