Ukuran Penyebaran Data – Bentuk dari suatu sistem ukuran penyebaran data yang merupakan sebuah indikator yang menunjukkan seberapa jauh data dari penyebaran suatu rata-rata.

Kali ini kabarkan.com akan memberikan pelajaran mengenai Ukuran Penyebaran Data. Dimana pelajaran ini akan dikupas secara jelas, dengan berdasarkan Pengertian, Makalah, Materi dan Contoh Soal .

Pengertian Ukuran Penyebaran Data

Daftar Isi Tampilkan

Bentuk dari suatu sistem ukuran penyebaran data yang merupakan sebuah indikator yang menunjukkan seberapa jauh data dari penyebaran suatu rata-rata. Distribusi data merupakan suatu bentuk pengukuran dalam materi statistik mencakup rentang, tumpang tindih, dan kuartil.

Yang Dimaksud Dengan Istilah Overlay Dan Kuartil, Berikut Penjelasannya:

Cakupan (rentang) adalah perbedaan antara nilai data terbesar dan nilai data yang terkecil.
Jarak tumpang tindih atau kuartil merupakan perbedaan antara kuartil atas (Q_ {3}) dan kuartil bawah (Q_ {1}).
Kuartil adalah pembagian jumlah data yang diurutkan menjadi angka yang sama untuk setiap bagiannya. Setiap bagian dipisahkan oleh kuartil, termasuk kuartil bawah (Q_ {1}), kuartil tengah (Q_ {2}) dan kuartil atas (Q_ {1}).

Rentengan Atau Jangkauan
Dalam data terpisah, nilai maksimum dan minimum dapat dengan mudah diketahui. lalu bagaimana dengan data grup? Bagaimana kita tahu nilai maksimum dan minimum? Nilai minimum dari data grup yang diperoleh dari titik tengah kelas pertama.

Akan tetapi bentuk dari suatu nilai maksimal dari data suatu kelompok didapat dari bentuk titik tengah pada ruang terkahir. Berikut ini adalah rumus dalam jangkauannya , Yakni :

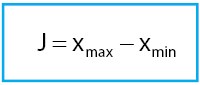
Overlay Atau Interquartile Reach
Kuartil bawah atau Q_ {1} dan nilai kuartil di atas Q_ {3} dalam data terpisah dibahas pada halaman bagaimanakah menemukan nilai kuartil. Demikian pula untuk kuartil nilai atas dan bawah dalam data grup. Dengan demikian, nilai volume data dapat dengan mudah ditemukan, yaitu.

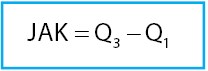
Data ini adalah data yang dibagi menjadi 4 bagian yang sama, dipisahkan oleh nilai kuartilnya tersebut Q_ {1}, Q_ {2} dan Q_ {3}.

Di bawah ini adalah tinjauan dari suatu data kuartil, yang mencakup penyimpangan, rata-rata kuartil, tiga rata-rata kuartil, dan lima seri statistik.

Penyimpangan kuartil atau sering juga disebut semi-kuartil adalah nilai-nilai yang mewakili setengah ruang. Diperoleh dengan mengurangi kuartil bawah dari kuartil atas, diikuti dengan membaginya dengan 2 (dua) bagian.
Kuartil rata-rata adalah bentuk kuartil atas dan kuartil bawah. Cara mendapatkan kuartil rata-rata, kita harus tambahkan kuartil atas dan kuartil bawah, lalu bagi dengan 2 (dua).
Rata-rata tiga kuartil adalah rata-rata yang terdiri dari kuartil atas, kuartil rata-rata, dan kuartil bawah. Cara mendapatkan kuartil rata-rata, tambahkan tiga kuartil, lalu bagi dengan 2 (dua).
Sedangkan statistik adalah data yang terdiri dari lima nilai, yaitu: nilai tertinggi (x_ {maks}), nilai terendah (x_ {min}), kuartil atas (Q_ {1}), dan kuartil rata-rata (Q_ {2 }) dan kuartil bawah (Q_ {3}).
Kesimpulan tentang penyimpangan ukuran, kuartil rata-rata, untuk tiga kuartil dan statistik untuk lima seri dapat dilihat pada tabel di bawah ini:

Makalah Ukuran Penyebaran Data

Statistik berasal dari bahasa Latin, yang berarti “status” atau negara. Awalnya, statistik berkaitan dengan fakta dan angka yang dikumpulkan oleh pemerintah untuk berbagai keperluan. Statistik juga berasal dari kata bahasa Inggris, yang merupakan negara bagian atau pemerintah.

Pemahaman statistik yang sangat sederhana adalah pengumpulan data dalam bentuk angka dan tersusun rapi dalam bentuk tabel, grafik, gambar dan lain-lain. Misalnya, tabel tentang status pekerja di kantor, grafik pertumbuhan populasi dari waktu ke waktu, dan sebagainya.

Sedangkan pemahaman yang lebih luas tentang statistik adalah seperangkat metode untuk mengumpulkan, menganalisis dan menafsirkan data dalam bentuk angka. Dan statistik juga angka yang menunjukkan sifat (karakteristik) dari data yang dikumpulkan.

Ukuran Penyebaran Data

Merupakan suatu bentuk dari tindakan penyebaran data (Maesures of Dispersion = Maesures of Variable) adalah berbagai indikator statistik yang dapat digunakan untuk menentukan tingkat penyebaran data (data Vasiasi = keseragaman = stabilitas data). [1]

Perbanyakan atau dispersi adalah pergerakan nilai yang diamati ke nilai rata-rata. Rata-rata himpunan nilai-nilai pengamatan tidak dapat ditafsirkan secara terpisah dari hasil penyebaran nilai-nilai ini di sekitar rata-rata. Semakin besar rentang nilai, semakin tidak representatif distribusi rata-rata.

Adapun ukuran penyebaran data yang biasanya dihitung, itu adalah rentang (range), standar deviasi (standar deviasi), kelebihan (peeling), asimetri (kemiringan). Rentang data menunjukkan perbedaan antara nilai tertinggi dan nilai terendah dalam kumpulan data.

Simpangan baku adalah nilai absolut dari selisih antara masing-masing nilai pengamatan dan nilai rata-rata dibagi dengan jumlah pengamatan. Kurtosis adalah ukuran untuk menentukan pola distribusi, yang biasanya dibandingkan dengan kurva distribusi normal.

Ukuran Penempatan Adalah Sebagai Berikut:

Ukuran spread dapat digunakan untuk menentukan apakah rata-rata benar-benar representatif atau tidak. Jika grup data memiliki distribusi rata-rata yang tidak rata, maka dikatakan bahwa mean tidak representatif.
Langkah-langkah penyebaran dapat digunakan untuk membandingkan variabilitas data.
Indikator penyebaran dapat membantu dengan penggunaan indikator statistik, misalnya, ketika menguji hipotesis, terlepas dari apakah dua sampel diperoleh dari populasi yang sama atau tidak.

Berbagai Langkah Untuk Menyebarluaskan Data

Dalam dunia statistik, ada beberapa jenis langkah untuk menyebarluaskan data, dari yang paling sederhana (paling kasar) hingga dimensi yang dianggap memiliki tingkat akurasi yang tinggi, yaitu: (1) rentang, (2) deviasi (mean deviasi),

Rentang

Ukuran pertama dari distribusi data yang disajikan di sini adalah Range, yang dikenal dalam dunia statistik sebagai ukuran paling sederhana dari distribusi data, itulah sebabnya ia juga sering disebut ukuran paling kasar dari distribusi data.

Definisi Kisaran

Kisaran biasa, yang ditunjukkan oleh simbol “R”, adalah salah satu indikator statistik yang menunjukkan variasi jarak antara peringkat terendah (peringkat) dan peringkat tertinggi (nilai) (peringkat tertinggi). Diringkas:
R = H – L
R = H – L

Ket:
R = rentang yang kami cari
H = skor atau nilai tertinggi (skor tertinggi)
L = peringkat atau peringkat terendah

Contoh Soal Ukuran Penyebaran Data

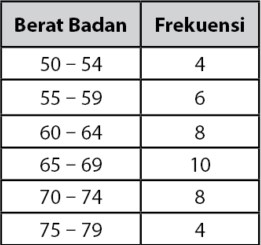
Hamparan dari data yang diberikan pada tabel di atas , yakni

A. 14,45
B. 14,95
C. 40,45
D. 41,45
E. 41,95

Keterangan :

Kuartil bawah = Q_{1}
Kuartil atas = Q_{3}

Jumlah data nya adalah:

=4+6+8+10+8+4

[ = 40 ]
=4+6+8+10+8+4Letak kuartil bawah berada di \frac{1}{4} bagian data dan letak kuartil atas berada di \frac{3}{4} bagian data.

Letak kuartil bawah:

\[ = \frac{1}{4} \times 40 \]
\[ = 10 \]

Letak kuartil atas:

\[ = \frac{3}{4} \times 40 \]
\[ = 30 \]

Simak tabel yang sudah kami dilengkapi dengan frekuensi komulatif kurang dari (fkk) serta letak kuartil bawah dan kuartil atas.

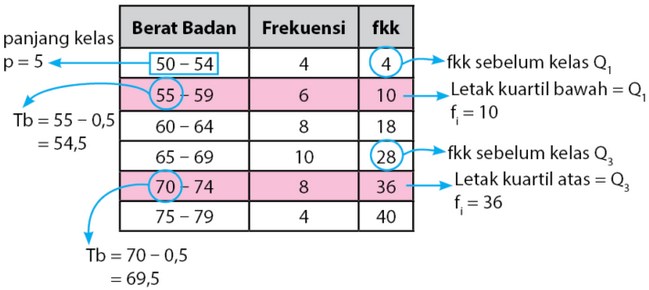
Cara mencari nilai kuartil bawah:

\[ Q_{1} = 54,5 + \left( \frac{\frac{1}{4} \cdot 40 - 4 }{36} \right) \times 5 \]
\[ Q_{1} = 54,5 + \left( \frac{10 - 4 }{36} \right) \times 5 \]
\[ Q_{3} = 54,5 + \left( \frac{6}{36} \right) \times 5 \]
\[ Q_{3} = 54,5 + 0,83 = 55,33 \]

Cara mencari nilai kuartil atas:

\[ Q_{3} = 69,5 + \left( \frac{\frac{3}{4} \cdot 40 - 28 }{36} \right) \times 5 \]
\[ Q_{3} = 69,5 + \left( \frac{30 - 28 }{36} \right) \times 5 \]
\[ Q_{3} = 69,5 + \left( \frac{2}{36} \right) \times 5 \]
\[ Q_{3} = 69,5 + 0,28 = 69,78 \]

Cara mencari nilai hamparan (H) atau jangakaun atar kuartil:

\[ H = Q_{3} - Q_{1} \]
\[ H = 69,78 - 55,33 \]
\[ H = 14,45 \]

Jawaban: A

Demikianlah sobat yang dapat kami sampaikan materi pelajaran ini. Semoga dengan apa yang telah kami sampaikan dalam artikel ini, dapat memberikan pemahaman serta bermanfaat untuk sobat semua. AMIN.

Baca Juga: