Dalam statistika, Standar Deviasi adalah salah satu konsep penting yang digunakan untuk mengukur sebaran atau dispersi data dalam suatu set data. Standar deviasi memberikan informasi tentang seberapa jauh titik data individu tersebar dari nilai rata-rata atau mean. Konsep ini memiliki peran penting dalam menganalisis data dan mengerti variasi yang terjadi dalam sebuah populasi atau sampel.

Pengertian Standar Deviasi

Daftar Isi Tampilkan

Standar deviasi ialah merupakan suatu nilai yang digunakan untuk menunjukkan ukuran dispersi atau variasi. Pada umumnya orang biasanya lebih memilih menggunakan standar deviasi daripada varian agar dapat mengetahui ukuran dispersi atau variasi.

Dalam kasus ini dikarenakan oleh nilai standar deviasi mempunyai satuan ukuran yang sama dengan satuan ukuran data sumbernya.

Maka semisalkan terdapat sebuah sampel data dengan satuan meter, maka nilai standar deviasinya juga memiliki satuan meter.

Namun pada, varian hanya mempunyai nilai satuan ukuran kuadrat, sehingga dalam hal ini nilainya menjadi meter kuadrat. Dalam ilmu statistika, standar deviasi ialah ukuran yang digunakan untuk mengukur jumlah variasi atau sebaran sejumlah nilai data.

Maka dapat disimpulkan, jika semakin rendah standar deviasi, maka akan semakin mendekati rata-rata, sedangkan apabila nilai standar deviasi semakin tinggi maka semakin lebar rentang variasi datanya.

Maka oleh sebab itu standar deviasi juga merupakan besar perbedaan dari nilai sampel terhadap rata-rata. Dan pada Standar deviasi juga dikenal juga dengan simpangan baku dan disimbolkan dengan alfabet Yunani sigma σ atau huruf Latin s.

Dalam bahasa Inggris, standar deviasi disebut standard deviation. Kemudian pada standar deviasi excel atau manual pada umumnya tidak mempunyai perbedaan yang signifikan. Dibawah ini ialah merupakan rumus standar deviasi yang mudah untuk dipahami.

Rumus Standar Deviasi

Untuk mengetahui cara menghitung standar deviasi baik manual ataupun standar deviasi excel, mari kita simak baik-baik rumus standar deviasi dibawah ini:

Rumus Standar Deviasi	S =√∑n ⁄ i = 1(xi – x¯)²/n-1 S = n∑n⁄i = 1 x ²i – (∑n = 1xi)²/n(n-1)
Keterangan	s = standar deviasi xi = nilai x ke i ∑= nilai rata-rata n = ukuran banyaknya data.

Standar deviasi biasanya disimbolkan dengan huruf s. Maka sebelum kita mencari nilai standar deviasi,langkah pertama yakni harus mengetahui terlebih dahulu nilai rata-rata data tersebut. Untuk lebih jelasnya maka perhatikan rumus standar deviasi atau simpangan baku pada gambar di atas.

Beberapa Fungsi Standar Deviasi dalam kehidupan :

Difungsikan guna membaca sebuah kecepatan detak jantung.
Mengukur tinggi badan.
Menghitung berat badan.
Digunakan untuk menentukkan jumlah resiko dan volatesitas terkait dengan investasi tertentu.
Difungsikan yakni untuk sebuah bahan guna mengambil suatu keputusan dalam konteks perisdustrian, misalnya : marketing, quality assurance, rekayasa produk, dan sebagainya.

Penghitungan Standar Deviasi

Penghitungan standar deviasi melibatkan beberapa langkah matematis yang perlu diikuti. Berikut adalah langkah-langkah umum dalam menghitung standar deviasi:

Hitung Rata-rata (Mean): Pertama, hitunglah nilai rata-rata dari seluruh data dalam sampel atau populasi.
Selisih dari Rata-rata: Kemudian, hitung selisih antara setiap titik data dengan nilai rata-rata. Langkah ini menggambarkan seberapa jauh setiap titik data dari nilai tengah.
Kuadrat Selisih: Kuadratkan masing-masing selisih yang dihitung pada langkah sebelumnya. Ini dilakukan untuk menghindari nilai selisih negatif dan untuk memberikan bobot lebih besar pada titik data yang jauh dari rata-rata.
Hitung Rata-rata Kuadrat Selisih: Hitunglah nilai rata-rata dari kuadrat selisih yang dihitung pada langkah sebelumnya. Langkah ini menghasilkan variansi, yang merupakan ukuran dispersi tanpa memperhitungkan satuan aslinya.
Hitung Akar Kuadrat: Akhirnya, hitunglah akar kuadrat dari variansi yang dihitung pada langkah sebelumnya. Inilah yang disebut sebagai standar deviasi. Ini mengembalikan ukuran dispersi dalam satuan aslinya.

Interpretasi Standar Deviasi

Interpretasi standar deviasi bergantung pada nilai yang ditemukan. Jika standar deviasi relatif kecil, maka data cenderung lebih dekat dengan rata-rata, sedangkan jika standar deviasi lebih besar, data cenderung lebih tersebar atau variatif. Beberapa poin penting untuk dipertimbangkan dalam menginterpretasi standar deviasi:

Rendah vs. Tinggi: Standar deviasi rendah menunjukkan konsentrasi data di sekitar nilai rata-rata, sementara standar deviasi tinggi menunjukkan variasi yang lebih besar dari nilai rata-rata.
Konteks: Penting untuk selalu menginterpretasikan standar deviasi dalam konteks masalah atau bidang tertentu. Nilai yang dianggap besar atau kecil dapat berbeda antara situasi yang berbeda.
Outliers: Standar deviasi juga dapat membantu dalam mengidentifikasi pencilan (outliers). Pencilan adalah nilai-nilai yang sangat berbeda dari mayoritas data, dan ini dapat dilihat dengan standar deviasi yang tinggi.

Kelebihan dan Kelemahan Standar Deviasi

Kelebihan Standar Deviasi:

Mengukur Variabilitas: Standar deviasi memberikan informasi yang kaya tentang variabilitas dalam data, yang penting dalam analisis dan pengambilan keputusan.
Penghitungan yang Umum: Penggunaan yang luas dan familiaritas dengan konsep standar deviasi membuatnya menjadi alat yang berguna untuk berkomunikasi dalam analisis data.

Kelemahan Standar Deviasi:

Sensitivitas Terhadap Outliers: Standar deviasi rentan terhadap pengaruh nilai-nilai ekstrem atau outlier, yang dapat memengaruhi interpretasi dispersi sebagaimana mestinya.
Tidak Menunjukkan Distribusi: Meskipun standar deviasi memberikan gambaran tentang sebaran data, itu tidak memberikan informasi tentang bentuk distribusi data.

Cara Menghitung Standar Deviasi Dengan Kalkulator

Cara menghitung standar deviasi selanjutnya dapat menggunakan kalkulator. Untuk perhitumgan ini tidak memerlukan rumus varian dan rumus standar deviasi khusus dalam menggunakan kalkulator. Untuk jenis kalkulator yang digunakan pun ialah jenis kalkulator scientific dan bukan yang biasanya. Dibawah ini terdapat beberapa langkah dalam menghitungnya yaitu sebagai berikut:

Langkah pertama ialah menyalakan kalkulator.
Tekan tombol Mode yang letaknya disamping tombol power pada kalkulator.
Tekan tombol No. 3 (STAT) untuk memilih mode statistik.
Selanjutnya tekan tombol No. 1 (VAR – 1)
Lalu masukkan data yang akan anda hitung dan tekan sama dengan (=), angka, sama dengan (=), dan seterusnya. Apabila data telah dimasukkan maka jangan lupa untuk menekan tombol sama dengan (=).
Tekan tombol AC.
Tekan tomol SHIFT
Kemudian STAT tekan (tombol nomor 1), VAR (tombol nomor 4), dan σ x (tombol nomor 3) untuk melihat hasil akhirnya.
Setelah itu diakhiiri dengan menekan tombol sama dengan (=).

Contoh Soal Standar Deviasi

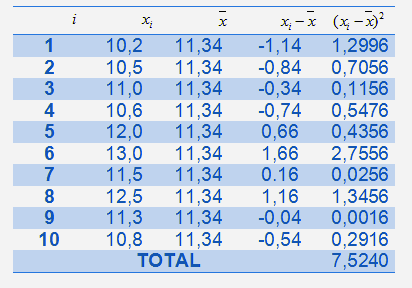
Setelah melakukan pengukuran intensitas cahaya sebanyak 10 kali pada halaman sekolah. Kemudian diperoleh data berturut-turut berikut ini: 10,2; 10,5;11,0;10,6;12,0;13,0;11,5;12,5;11,3 dan 10,8 W/m2.Jawab

Pertama-tama kita tulis datanya di dalam tabel (supaya mudah kita bisa melakukan perhitungan menggunakan Microsoft Excel).

Setelah itu gunakan persamaan atau rumus ragam sampel

Fungsi dan Manfaat Standar Deviasi

Fungsi dan Manfaat Standar Deviasi dalam Analisis Data

Standar deviasi adalah salah satu ukuran statistik yang memiliki banyak fungsi dan manfaat dalam analisis data. Ini digunakan untuk mengukur sebaran data di sekitar rata-rata, dan memiliki peran kunci dalam memberikan wawasan tentang variasi data dalam suatu populasi atau sampel. Berikut ini adalah beberapa fungsi dan manfaat utama dari standar deviasi:

1. Mengukur Variabilitas Data

Fungsi utama dari standar deviasi adalah mengukur sejauh mana data tersebar dari nilai rata-rata. Semakin tinggi standar deviasi, semakin besar variasi data. Ini membantu kita memahami seberapa stabil atau tidak stabil data dalam konteks tertentu. Misalnya, dalam analisis ekonomi, standar deviasi dari harga saham dapat memberi tahu seberapa besar fluktuasi harga dari waktu ke waktu.

2. Identifikasi Pencilan (Outliers)

Standar deviasi juga membantu dalam mengidentifikasi pencilan atau nilai-nilai ekstrem yang jauh dari nilai rata-rata. Pencilan dapat memberikan wawasan tentang situasi atau kasus yang tidak biasa dalam data. Dengan memperhatikan nilai-nilai yang memiliki deviasi yang tinggi, kita dapat mengevaluasi apakah ada faktor khusus yang mempengaruhi data tersebut.

3. Pengukuran Ketepatan Model Statistik

Dalam statistika, seringkali kita menggunakan model matematika untuk meramalkan atau menjelaskan data. Standar deviasi dapat digunakan untuk mengukur seberapa akurat model tersebut dalam memprediksi data baru. Semakin rendah standar deviasi residu (selisih antara nilai yang dihitung oleh model dan nilai aktual), semakin baik model statistik tersebut.

4. Perbandingan Data Antara Grup atau Sub-populasi

Ketika kita memiliki beberapa kelompok atau sub-populasi dalam data, standar deviasi dapat membantu dalam membandingkan tingkat variasi antara kelompok-kelompok tersebut. Ini dapat membantu dalam mengidentifikasi kelompok yang memiliki tingkat konsistensi yang lebih tinggi atau lebih rendah dalam suatu atribut tertentu.

5. Pengambilan Keputusan

Standar deviasi juga memiliki manfaat dalam pengambilan keputusan. Misalnya, dalam industri manufaktur, standar deviasi dapat membantu mengukur kualitas dan konsistensi produk. Dalam pengelolaan investasi, standar deviasi dapat membantu investor memahami risiko yang terkait dengan portofolio investasi.

6. Penelitian Ilmiah

Dalam penelitian ilmiah, standar deviasi digunakan untuk melaporkan variasi dalam hasil eksperimen atau observasi. Ini membantu ilmuwan dan peneliti dalam menilai seberapa dapat diandalkan atau bervariabilitas hasil penelitian mereka.

Kesimpulan

Standar deviasi adalah alat statistik yang penting untuk memahami sebaran data dalam suatu sampel atau populasi. Dengan menghitung standar deviasi, kita dapat mendapatkan wawasan tentang sejauh mana data tersebar dari nilai rata-rata. Meskipun memiliki kelebihan dan kelemahan, standar deviasi tetap menjadi alat yang berharga dalam analisis statistik dan pengambilan keputusan. Namun, dalam menginterpretasikan hasil standar deviasi, selalu perhatikan konteks dan karakteristik khusus dari data yang sedang Anda analisis.