SPLDV – Setelah sebelumnya ContohSoal.co.id telah membahas materi tentang SPLTV. Maka dipertemuan kali ContohSoal.co.id akam menerangkan materi tentang SPLDV beserta pengertian, metode grafik rumus dan contoh soalnya. Untuk lebih jelasnya mari simak ulasan dibaah ini.

Pengertian SPLDV

Daftar Isi Tampilkan

SPLDV(sistem persamaan linear dua variabel) ialah merupakan suatu bentuk relasi sama dengan dalam bentuk aljabar berpangkat satu dan apabila digambarkan dalam sebuah grafik maka akan membentuk garis lurus.

Ciri – Ciri SPLDV

Menggunakan relasi tanda sama dengan ( = )
Memiliki dua variabel
Kedua variabel tersebut memiliki derajat satu ( berpangkat satu )

Hal Berhubungan Dengan SPLDV

Suku

Suku yakni bagian dari suatu bentuk aljabar yang terdiri dari variabel, koefisien dan konstanta. Dan setiap suku di yakni dengan tanda baca penjumlahan ataupun pengurangan

Contoh :

6x – y + 4 , maka suku – suku dari persamaan tersebut ialah 6x , -y dan 4

Variabel

Variabel , yakni perubah atau pengganti suatu bilangan yang biasanya dilambangkan dengan huruf seperti x dan y

Contoh :Mika memiliki 2 buah nanas dan 5 buah jeruk. Jika dituliskan dalam bentuk persamaan ialah

Nanas = x
Jeruk = y
Persamannya ialah2x + 5y

Koefisien

Koefisien ialah merupakan suatu bilangan yang menyatakan banyaknya suatu jumlah variabel yang sejenis.

Contoh :Mika memiliki 2 buah nanas dan 5 buah jeruk. Jika di tulis dalam bentuk persamaan ialah:

Jawab :

Nanas = x dan Jeruk = y
Persamannya ialah 2x + 5y
Dimana 2 dan 5 ialah koefisien. Dan 2 ialah koefisien x dan 5 yakni koefisien y

Konstanta

Konstanta yakni bilangan yang tidak diikuti dengan variabel, maka nilainya tetap atau konstan untuk berapapun nilai perubahnya

Contoh :

2x+5y+7,dari persamaan tersebut konstanta ialah 7 , sebab 7 merupakan nilai yang tidak terpengaruh dengan berapapun variabelnya

Itulah beberapa hal yang berhubungan tentang bentuk umum spldv untuk kita pahami sebelum kita memahami tentang rumus spldv.

Syarat Sistem Persamaan Linier Dua Variabel dapat memiliki satu penyelesaian, yakni:

Terdapat dua persamaan linier dua variabel sejenis
Persamaan linier dua variabel yang membentuk sistem persamaan linier dua variabel, bukan persamaan linier dua variabel yang sama

Metode SPLDV dengan Grafik

Grafik dari persamaan linear dua variabel ax + by = c ialah garis lurus.
Penyelesaian SPLDV ax + by = c
px + qy = r

ialah merpakan titik potong antara garis ax + by = c dan garis px + qy = r.

Langkah-langkah untuk menentukan penyelesaian SPLDV dengan menggunakan metode grafik ialah sebagai berikut:

Pada titik potong garis tentukanlah dengan sumbu X, syarat y=0,
Dan pada titik potong garis tentukanl juga sumbu Y, syarat x = 0,
Langkah (1) dan (2) dapat disederhanakan dalam bentuk tabel sebagai berikut:
gambar garis dari setiap persamaan,
Dari kedua garis tentukanlah titik potongn penyelesaian SPLDV.

Pada gambar dibawah ini merupakan Grafik dari persamaan linear dua variabel berbentuk garis lurus.

Secara umum , ada 4 langkah untuk menyelesaiakan permasalahan SPLDV dengan menggunakan metode grafik. Keempat langkah tersebut ialah, Agar lebih memahaminya, perhatikan contoh berikut.

Pada suatu acara konser , telah terjual karcis kelas I dan II sebanyak 500 lembar. Harga karcis kelas I yakni Rp 8.000,00, sedangkan harga karcis II ialah Rp 6.000,00.

Apabila hasil penjualan seluruh karcis Rp 3.250.000,00, maka tentukan banyak karcis masing-masing kelas I dan II yang terjual.

Langkah pertama ialah mengubah kalimat-kalimat pada soal cerita di atas menjadi model matematika, sehingga membentuk sistem persamaan linear.

Jika terjualnya karcis secara berturut yakni x dan y, maka kalimat “dalam sebuah konser , terjual karcis kelas I dan kelas II sebanyak 500 lembar,” dapat dimodelkan menjadi, x+y=500

Namun dengan kalimat, “Harga karcis kelas I ialah Rp 8.000,00, serta harga kelas II ialah Rp 6.000,00. Jika hasil penjualan seluruh karcis ialah Rp 3.250.000,00,”

Sehingga diperoleh SPLDV sebagai berikut.

x+y=500

8.000x+6.000y=3.250.000

Langkah kedua, cari terlebih dahulu koordinat dari dua titik yang dilewati oleh grafik masing-masing persamaan tersebut. Pada umumnya,dari dua titik yang telah dipilih tersebut merupakan titik potong grafik persamaan dengan sumbu-x dan -y.

x +y = 500

x = 0 ⇒ 0 + y = 500

⇔ y = 500

y = 0 ⇒ x + 0 =500

⇔ x =500

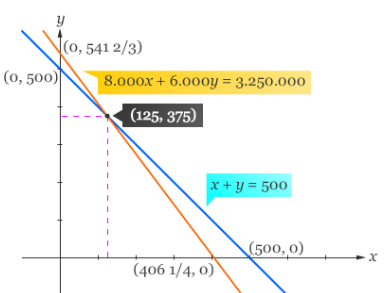
Maka pada grafik persamaan x + y = 500 memotong sumbu-x di (500, 0) dan sumbu-y di (0, 500).

Contoh Soal SPLDV

Tentukan Himpunan penyelesaian dari persamaan x + 3y = 15 dan 3x + 6y = 30Penyelesaian :

Diketahui :

Persamaan 1 = x + 3y = 15
Persamaan 2 = 3x + 6y = 30

Langkah Pertama yakni denagn menentukan variabel mana yang akan di eliminasi terlebih dahulu. Kali ini kita akan menghilangkan x terlebih dahulu, dan supaya kita temukan nilai y . Caranya yakni:

3x + 6y = 30 : 3
x + 2y = 10 . . . . ( 1 )
x + 3y = 15 . . . .(2)

Kemudian yang kedua pada persamaan (1) dan (2), mari kita eliminasi, sehingga hasilnya :

x + 3y = 15
x + 2y = 10 _
y = 5

Terkahir yang ketiga, guna mengetahui nilai x , maka caranya sebagai berikut :

x + 3y = 15 | x2 | <=> 2x + 6y = 30 . . . .( 3 )
3x + 6y = 30 | x1 | <=> 3x + 6y = 30 . . .. (4 )

Pada eliminasi dari persamaan (3) dan (4 ), yakni hasilnya menjadi :

3x + 6y = 30
2x + 6y = 30 _
x = 0

Maka, Himpunan penyelesaiannya ialah HP = { 0 . 5 }

Demikianlah materipembahasan kali ini mengenai SPLDV, semoga artikel ini dapat bermanfaat bagi sobat semua

Artikel Lainnya: