Persamaan Garis Singgung Lingkaran – Setelah sebelumnya ContohSoal.co.id telah membahas materi tentang Bentuk Akar. Maka dipertemuan kali ini ContohSoal.co.id akan membahas materi tentang Persamaan garis singgung lingkaran. Untuk lebih lengkapnya simak ulasan yang sudah ContohSoal.co.id rangkum dibawah ini.
Pengertian Garis Singgung
Dalam ilmu geometri, garis singgung atau biasa disebut juga garis tangen kurva bidang pada titik yang diketahui ialah garis lurus yang “hanya menyentuh” kurva pada titik tersebut.
Namun leibniz mendefinisikan bahwa suatu garis singgung merupakan suatu garis yang melalui sepasang titik tak hingga dekat pada kurva.
Lebih tepatnya, garis lurus ini disebut juga menyinggung kurva y = f (x) di titik x = c pada kurva apabila garis melalui titik (c, f (c)) pada kurva mempunyai kemiringan f ‘(c)dan f ‘ialah turunan f. Definisi yang serupa juga digunakan pada kurva ruang dan kurva dalam ruang Euklides dimensi –n.
Sebab melalui titik di mana garis singgung dan kurva bertemu, maka disebut titik singgung, kemudian pada garis singgung “mempunyai arah yang sama” dengan kurva, dan dengan demikian merupakan pendekatan garis lurus terbaik pada kurva pada titik tersebut.
Serupa dengan garis singgung, bidang singgung permukaan pada titik yang diketahui ialah bidang yang “hanya menyentuh” permukaan di titik tersebut.
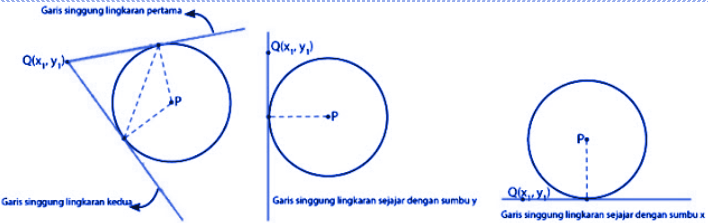
Garis Singgung Melewati Sebuah Titik Lingkaran
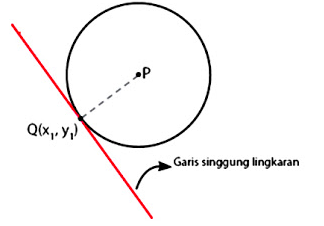
Rumus persamaan garis singgung lingkaran yang pertama berkaitan dengan garis singgung yang melewati sebuah titik pada lingkaran. Dalam garis singgung ini terdapat sebuah titik pusat P pada lingkaran.
Kemudian titik Q dengan koordinat x dan y ingin menyinggung lingkaran tersebut. Untuk itu cara mencari garis singgung yang melalui titik Q terhadap lingkaran tersebut diperlukan persamaan lingkaran agar titik Q dan P dapat saling menyinggung. Perhatikan gambar di bawah ini!
| Persamaan Lingkaran | Persamaan Garis Singgung |
| x² + y² = r² | xx¹ + yy¹ = r² |
| (x – h)² + (y – k)² = r² | (x -h )(x¹ – h) + ( y – k) (y¹ -k) = r² |
| x² + y² + Ax + By + C = r² | xx¹ + yy¹ +¹/²A(x + x¹)¹/²B ( y + y¹) + C = r² |
Agar dapat menentukan garis singgung dengan melalui sebuah titik pada lingkaran di atas bisa menggunakan beberapa persamaan umum.
Bentuk persamaan lingkaran yang diketahui tersebut akan mempengaruhi penggunaan rumusnya. Adapun rumus persamaan garis singgung yang melewati sebuah titik yaitu sebagai berikut:
Garis Singgung Melewati Sebuah Titik di Luar Lingkaran
Rumus persamaan garis singgung selanjutnya berkaitan dengan garis singgung yang melewati sebuah titik di luar lingkaran. Jenis garis singgung tersebut dapat dinamakan dengan garis singgung polar atau garis singgung kutub.
Garis singgung pada lingkaran dapat dicari apabila diluar lingkaran terdapat titik (x, y) dengan cara menarik garis lurus menuju titik tadi. Dengan begitu garisnya dapat menyinggung lingkarannya. Untuk lebih jelasnya dapat anda perhatikan gambar di bawah ini:
Mencari persamaan lingkaran yang garis singgungnya menggunakan konsep permisalan. Adapun rumusnya yakni y – y1 = m (x – x1), dimana x dan y ialah titik yang dilalui oleh garis singgung di luar lingkaran.
Sedangkan m aalah gradien.Cara menentukan persamaan garis singgung yang melewati titik diluar lingkaran tersebut menggunakan beberapa langkah penting. Adapun langkah langkahnya ialah sebagai berikut:
- Setelah itu nilai y disubstitusikan ke persamaan lingkaran di atas sehingga memperoleh variabel x pada persamaan kuadrat.
- Agar dapat menemukan persamaan garis singgung selanjutnya ialah mencari nilai diskriminan pada persamaan kuadratnya. Maka nilai D = 0 untuk membuat garis yang dapat menyinggung lingkarannya.
- Langkah selanjutnya ialah menyelesaikan persamaan kuadrat pada langkah sebelumnya.
- Kemudian substitusikan pada persamaan lingkaran y – y1 = m (x – x1).
Contoh Soal Garis Singgung Lingkaran
Tentukan persamaan garis singgung lingkaranx2+y2=40.dengan gradien 3
Jawab :
m=3,R2=40.maka.R=√40
Jadi
- y= mx±R√(1+m2)
- y=3x±√40√(1+32)
- y=3x±√40√10
- y=3x±√400
- y=3x±20
- y=3x+20atau.y=3x – 20
Contoh Soal.2
Tentukan persamaan garis singgung lingkaran (x–2)2+(y+3)2 =125.dengan gradien.2
Jawab :
m=1,R2=125.makaR=5√5
Jadi
- y+3= m(x–2) ± R√(1+m2)
- y+3= 2(x–2) ±5√5√(1+ 22)
- y+3= 2x–4 ±5√5√5
- y=2x–7±25
- y=2x–7+25.atau y=2x–7-25
- y=2x+18 atau y = 2x – 32
Contoh Soal.3
Carilah persamaan garis singgung pada lingkaran.x2+y2 =50 yang membentuk sudut 45o dengan sumbu x positif
Jawab :
m=tan.45o=1,R2=50.maka R =√50
Jadi
- y=mx±R√(1 + m2)
- y=x ±√50√(1 + 12)
- y=x ±√50√2
- y=x ±√100
- y= x ± 10
- y= x+10 atau y=x–10
Demikianlah materi pembahasan kali ini mengenai persamaan garis singgung lingkaran, semoga artikel ini bermanfaat bagi sobat semua.
Artikel Lainnya: