Limas Segitiga – Materi pembahasan kali ini masih seputar mengenai materi matematika yakni, limas segitiga beserta pengertian, rumus, beraturan dan contoh soalnya. Namun dipertemuan sebelumnya ContohSoal.co.id juga telah menerangkan mengenai materi Prisma. Baiklah unuk lebih jelasnya sobat dapat simak ulasannya berikut ini.
Pengertian Limas
Apa itu Limas?ialah merupakan bangun ruang yang mempunyai sebuah alas berbentuk (segitiga, segi empat, atau segi lima) bidang sisi tegaknya memiliki bentuk segitiga yang berpotongan pada satu titik.
Adapun pada titik potong dari sisi-sisi tegak limas di sebut dengan titik puncak limas
Ciri-Ciri Limas Segitiga
- Mempunyai alas yang membentuk segitiga.
- Mempunyai 4 empat bidang pada sisi yakni alas dan tiga buah sisi tegak.
Rumus limas segitiga
Rumus Luas Alas Limas
| Rumus Luas Alas Limas |
|
Rumus Luas Permukaan Limas
| Rumus Luas Permukaan Limas |
|
Rumus Volume Limas Segitiga
| Rumus Volume Limas Segitiga |
|
Jenis-Jenis Limas
Berdasarkan bentuk alasnya, limas dapat dibagi menjadi beberap jenis, yakni ;
-
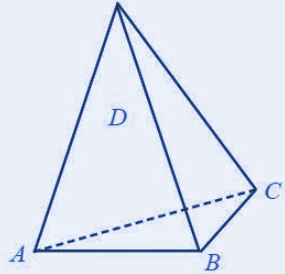
Limas Segitiga
Limas segitiga ialah merupakan sebuah bangun yang mempunyai alas dengan bentuk segitiga (baik segitiga sama kaki, segitiga sama sisi, segitiga siku-siku, maupun segitiga sembarang).
Perhatikan gambar di bawah ini!
-
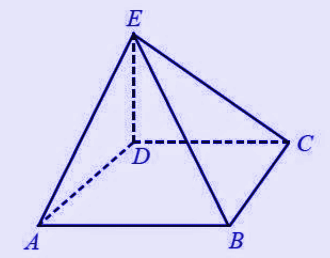
Limas Segiempat
Limas segi empat ialah merupakan sebuah bangun yang mempunyai alas dengan bentuk segi empat (baik berupa persegi, persegi panjang, trapesium, belah ketupat, layang-layang, jajaran genjang dan lainnya).
Perhatikan gambar berikut ini!
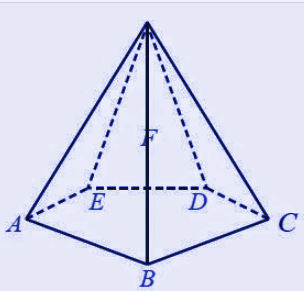
Limas segi lima ialah merupakan sebuah bangun yang mempunyai alas dengan bentuk segi lima, baik segilima teratur maupun segi lima sembarang.
Perhatikan gambar berikut ini!
-
Limas Segilima
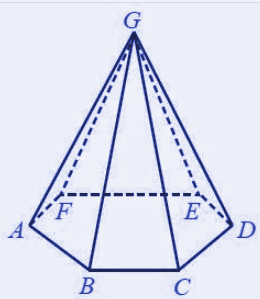
Limas segi enam ialah limas yang memiliki alas berbentuk segi enam baik segi enam teratur maupun sembarang. Perhatikan contoh berikut ini!
-
Limas Segi enam
Contoh Soal Limas Segitiga
Contoh Soal 1
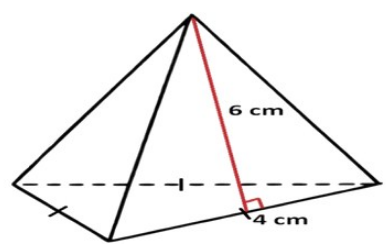
Perhatikan gambar di bawah ini dan carilah nilai dari luas permukaan limas segitiga sama sisi tersebut ?
Jawab :
Ppanjang sisi alasnya = 4 cm dan tinggi untuk sisi tegak = 6
maka :
- Luas Permukaan = 1/4 s2√3 + 3 2 s . h
- Luas Permukaan = 4√3 + 36
- Luas Permukaan = 4(√3 + 9)
Contoh Soal .2
Apabila telah diketahui luas permukaan limas segitiga sama sisi ialah 9(√3 + 10 ). Dan luas alas dari limas ialah 9√3, Maka tentukanlah tinggi sisi tegaknya ?.Pembahasan
- Luas Alas = 1/4 s2√3
- 1/4 s2√3 = 9√3
- s2√3 = 36√3
- s2= 36 √3 √3
- s2= 36
- s = 6 cm
Maka, panjang sisi alas ialah 6 cm. Sudah diketahui luas permukaan, luas sisi alas maka sekarang bisa mencari tinggi pada sisi tegak dengan rumus :
Luas Permukaan
- = 1/4 s2√3 + 3/2 s . h
- 9(√3 + 10 ) = 9√3 + 3 2
- 6 . h
- 9√3 + 90 = 9√3 + 9h
- 9h = 9√3 + 90 – 9√3
- 9h = 90
- h = 90/9 = 10 cm
Maka, tinggi untuk sisi tegaknya ialah 10 cm.
Contoh Soal 3
Alas sebuah limas berbentuk segitiga sama sisi dengan panjang sisinya 10 cm Maka hitunglah volume limas tersebut apabila diketahui tinggi limas tersebut 12 cm!
Penyelesaian:
Dengan menggunakan cara cepat maka luas alas limas yang berbentuk segi tiga sama sisi yakni:
- LΔ = ¼√3.s2
- LΔ = ¼√3.(10 cm)2
- LΔ = 25√3 cm2
Volume limas yakni:
- V = 1/3 × LΔ × t
- V = 1/3 × 25√3 cm2 × 12 cm
- V = 100√3
Contoh Soal 4
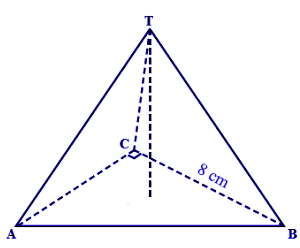
Apabila telah diketahui limas segitiga siku-siku T.ABC seperti gambar di bawah ini.
Apabila volume limas tersebut ialah 96 cm3 dan tingginya 12 cm, maka tentukan:
- luas alas limas tersebut,
- panjang AC dan AB
Penyelesaian:
a) Volume limas dapat dicari dengan persamaan:
- V = 1/3 × L.alas × tinggi
- 96 cm3 = 1/3 × L.alas × 12 cm
- L.alas = 96 cm3/4 cm
- L.alas = 24 cm2
b)Untuk mencari panjang AC gunakaan rumus luas segitiga dimana luas L.ΔABC sama dengan luas alas limas, sedangkan untuk mencari panjang AB gunakan theorema phytagoras.
- L.ΔABC = ½ × AC × BC
- 24 cm2 = ½ × AC × 8 cm
- AC = 6 cm
- AB2 = AC2 + BC2
- AB2 = (6 cm)2 + (8 cm)2
- AB2 = 36 cm2 + 64 cm2
- AB2 = 100 cm2
- AB = √(100 cm2)
- AB = 10 cm
Demikianlah materi pembahasan kali ini tentang lims segitiga, semoga bermanfaat.
Artikel Lainnya: