Bilangan Bulat – Pengertian, Operasi, Penjumlahan & Contoh Soal

Bilangan bulat adalah jenis bilangan yang terdiri dari angka-angka bulat tanpa adanya bagian pecahan. Bilangan bulat dapat dinyatakan dalam bentuk positif atau negatif, namun tidak mengandung bagian desimal. Contoh bilangan bulat positif adalah 1, 2, 3, 4, dan seterusnya, sedangkan contoh bilangan bulat negatif adalah -1, -2, -3, -4, dan seterusnya.

Nol juga termasuk ke dalam jenis bilangan bulat. Bilangan bulat digunakan dalam berbagai aplikasi matematika, fisika, dan teknologi. Sifat-sifat bilangan bulat, seperti penjumlahan, pengurangan, perkalian, dan pembagian, dapat digunakan untuk melakukan operasi matematika pada bilangan bulat.

Mengenal Tentang Apa Itu Bilangan Bulat?

 Bilangan Bulat ialah merupakan suatu bilangan yang terdiri dari bilangan bulat positif, bilangan nol serta bilangan bulat negatif. Selanjutnya bilangan ini jug merupakan bagian dari bilangan cacah(0,1,2,3,..) dan negatifnya (-1,-2,-3, …; -0 ialah sama dengan 0 sehingga tidak lagi dimasukkan secara terpisah).

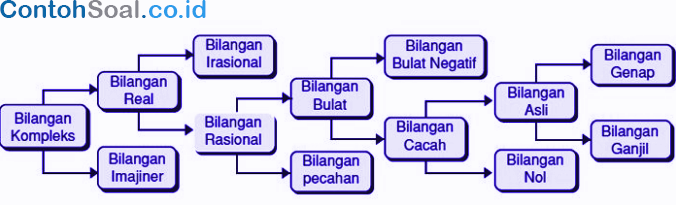
Agar dapat lebih memahami lebih jelas lmaka simak gambar struktur bilangan di bawah ini.

Dari pengertian di atas bisa kita ambil kesimpulan jika bilangan bulat ialah merupakan suatu himpunan bilangan yang termasuk didalamnya ialah bilangan cacah, asli, prima, komposit, nol, satu, negatif, ganjil dan bilangan genap. Namun bukan hanya itu saja yang mana pada bilangan bulat tidak mempunyai bilangan terkecil ataupun bilangan terbesar.

Mengetahui Tentang Sifat Sifat Bilangan Bulat

Bilangan bulat memiliki banyak sifat yang penting dalam matematika. Beberapa sifat bilangan bulat yang paling mendasar antara lain:

1. Sifat Komutatif

Sifat komutatif menyatakan bahwa hasil operasi matematika pada dua bilangan bulat tidak bergantung pada urutan bilangan tersebut. Dalam operasi penjumlahan dan perkalian, sifat ini dapat dituliskan sebagai berikut:

• a + b = b + a
• a x b = b x a

2. Sifat Asosiatif

Sifat asosiatif menyatakan bahwa hasil operasi matematika pada tiga bilangan bulat tidak bergantung pada urutan pengelompokan bilangan tersebut. Dalam operasi penjumlahan dan perkalian, sifat ini dapat dituliskan sebagai berikut:

• (a + b) + c = a + (b + c)
• (a x b) x c = a x (b x c)

3. Sifat Distributif

Sifat distributif menyatakan bahwa hasil perkalian bilangan dengan jumlah bilangan lain dapat didekomposisi menjadi jumlah hasil perkalian dari bilangan tersebut dengan setiap bilangan. Dalam operasi penjumlahan dan perkalian, sifat ini dapat dituliskan sebagai berikut:

• a x (b + c) = (a x b) + (a x c)

4. Sifat Identitas

Sifat identitas menyatakan bahwa hasil operasi matematika pada bilangan bulat dengan bilangan nol dan bilangan satu selalu menghasilkan bilangan yang sama dengan bilangan itu sendiri. Dalam operasi penjumlahan dan perkalian, sifat ini dapat dituliskan sebagai berikut:

• a + 0 = a
• a x 1 = a

5. Sifat Invers

Sifat invers menyatakan bahwa setiap bilangan bulat memiliki kebalikan atau inversnya, yaitu bilangan yang jika ditambahkan pada bilangan tersebut menghasilkan nol. Dalam operasi penjumlahan dan pengurangan, sifat ini dapat dituliskan sebagai berikut:

• a + (-a) = 0

6. Sifat Urutan

Sifat urutan menyatakan bahwa dalam sebuah rangkaian bilangan bulat yang terurut, bilangan yang lebih besar akan selalu mengikuti bilangan yang lebih kecil. Dalam sifat ini, bilangan-bilangan tersebut dapat diurutkan dari yang terkecil hingga yang terbesar atau sebaliknya.

7. Sifat Bilangan Prima

Bilangan prima hanya memiliki dua faktor yang positif, yaitu satu dan bilangan itu sendiri. Karena sifat ini, bilangan prima sangat penting dalam kriptografi, yang merupakan studi tentang teknik pengamanan informasi.

8. Sifat Bilangan Ganjil dan Genap

Bilangan ganjil tidak dapat dibagi habis oleh dua, sedangkan bilangan genap dapat dibagi habis oleh dua. Karena sifat ini, bilangan ganjil dan genap dapat digunakan untuk memodelkan banyak hal dalam matematika, seperti jumlah benda atau jumlah hal yang dapat dibagi dengan rata.

Mengenal Tentang Beragam Jenis Jenis Bilangan Bulat

1. Bilangan Bulat Positif

Bilangan bulat positif adalah bilangan bulat yang nilainya lebih besar dari nol. Bilangan bulat positif dapat diwakili dengan angka 1, 2, 3, 4, dan seterusnya. Bilangan bulat positif digunakan dalam berbagai aplikasi matematika, seperti dalam menghitung jarak, kecepatan, waktu, dan lain sebagainya. Bilangan bulat positif juga sering digunakan dalam statistik untuk merepresentasikan data positif seperti jumlah pendapatan atau usia.

2. Bilangan Bulat Negatif

Bilangan bulat negatif adalah bilangan bulat yang nilainya lebih kecil dari nol. Bilangan bulat negatif dapat diwakili dengan angka -1, -2, -3, -4, dan seterusnya. Bilangan bulat negatif juga digunakan dalam berbagai aplikasi matematika, seperti dalam menghitung debit air, suhu, dan sebagainya. Dalam pengolahan data, bilangan bulat negatif sering digunakan untuk merepresentasikan data yang memiliki nilai negatif, seperti saldo akun atau pengeluaran.

3. Bilangan Nol

Nol adalah bilangan bulat yang nilainya sama dengan nol. Nol dapat digunakan sebagai pengukur titik awal atau sebagai nilai tengah dalam perhitungan. Misalnya, dalam suatu eksperimen, suhu nol dalam skala Celcius digunakan sebagai titik awal untuk mengukur suhu di bawah nol. Dalam matematika, nol sering digunakan dalam operasi matematika, seperti dalam operasi penjumlahan, pengurangan, perkalian, dan pembagian.

4. Bilangan Bulat Genap

Bilangan bulat genap adalah bilangan bulat yang habis dibagi dua. Contohnya adalah 2, 4, 6, 8, dan seterusnya. Bilangan bulat genap dapat dibentuk dari perkalian bilangan bulat dengan 2. Misalnya, 2 × 1 = 2, 2 × 2 = 4, 2 × 3 = 6, dan seterusnya. Bilangan bulat genap sering digunakan dalam matematika untuk memodelkan jumlah benda atau jumlah hal yang dapat dibagi dengan rata.

5. Bilangan Bulat Ganjil

Bilangan bulat ganjil adalah bilangan bulat yang tidak habis dibagi dua. Contohnya adalah 1, 3, 5, 7, dan seterusnya. Bilangan bulat ganjil dapat dibentuk dari bilangan bulat genap dengan menambahkan satu. Misalnya, 1 + 1 = 2, 3 + 1 = 4, 5 + 1 = 6, dan seterusnya. Bilangan bulat ganjil sering digunakan dalam matematika untuk memodelkan jumlah benda atau jumlah hal yang tidak dapat dibagi dengan rata.

6. Bilangan Prima

Bilangan prima adalah bilangan bulat yang hanya memiliki dua faktor, yaitu 1 dan bilangan itu sendiri. Contohnya adalah 2, 3, 5, 7, 11, 13, dan seterusnya. Bilangan prima sering digunakan dalam kriptografi, yang merupakan studi tentang teknik pengamanan informasi.

Menjabarkan Tentang Rangkaian Operasi Hitung Soal Bilangan Bulat

1. Operasi Penjumlahan Bilangan Bulat

Operasi penjumlahan bilangan bulat adalah proses untuk menambahkan dua atau lebih bilangan bulat untuk mendapatkan hasil akhir. Operasi ini dapat dilakukan pada bilangan bulat positif, negatif, atau keduanya.

Untuk melakukan operasi penjumlahan bilangan bulat, kita perlu mengetahui aturan-aturan berikut:

• Jika kedua bilangan memiliki tanda yang sama (keduanya positif atau keduanya negatif), maka kita dapat menambahkan kedua bilangan dan menjaga tanda mereka sebagai tanda hasilnya.
  Contoh: 3 + 5 = 8, -2 + (-6) = -8

• Jika kedua bilangan memiliki tanda yang berbeda, maka kita dapat mengurangkan bilangan yang memiliki nilai absolut lebih kecil dari bilangan yang memiliki nilai absolut lebih besar. Hasilnya akan memiliki tanda dari bilangan yang memiliki nilai absolut lebih besar.
  Contoh: 7 + (-4) = 3, -8 + 3 = -5

• Jika kita menambahkan banyak bilangan bulat, kita dapat menambahkan mereka satu per satu, dengan mempertahankan tanda setiap bilangan.
  Contoh: 2 + 4 + (-3) + 5 = 8

• Penjumlahan bilangan bulat juga bersifat komutatif, artinya urutan bilangan yang dijumlahkan tidak mempengaruhi hasil penjumlahan.
  Contoh: 2 + 3 + (-1) = 4 dan (-1) + 3 + 2 = 4

• Penjumlahan bilangan bulat juga bersifat asosiatif, artinya urutan pengelompokan bilangan yang dijumlahkan tidak mempengaruhi hasil penjumlahan.
  Contoh: (4 + 2) + (-1) = 5 dan 4 + (2 + (-1)) = 5

• Bilangan bulat nol (0) adalah elemen identitas untuk penjumlahan, yaitu penjumlahan bilangan bulat apa pun dengan nol akan menghasilkan bilangan bulat itu sendiri.
  Contoh: 5 + 0 = 5 dan (-8) + 0 = -8

2. Operasi perkalian Bilangan bulat

Operasi perkalian bilangan bulat adalah proses untuk mengalikan dua atau lebih bilangan bulat untuk mendapatkan hasil akhir. Operasi ini dapat dilakukan pada bilangan bulat positif, negatif, atau keduanya.

Untuk melakukan operasi perkalian bilangan bulat, kita perlu mengetahui aturan-aturan berikut:

• Jika kedua bilangan memiliki tanda yang sama (keduanya positif atau keduanya negatif), maka kita dapat mengalikan kedua bilangan dan menjaga tanda mereka sebagai tanda hasilnya.
  Contoh: 3 x 5 = 15, (-2) x (-6) = 12

• Jika kedua bilangan memiliki tanda yang berbeda, maka hasil perkaliannya akan negatif.
  Contoh: 7 x (-4) = -28, (-8) x 3 = -24

• Jika kita mengalikan banyak bilangan bulat, kita dapat mengalikan mereka satu per satu, dengan mempertahankan tanda setiap bilangan.
  Contoh: 2 x 4 x (-3) x 5 = -120

• Perkalian bilangan bulat juga bersifat komutatif, artinya urutan bilangan yang dikalikan tidak mempengaruhi hasil perkalian.
  Contoh: 2 x 3 x (-1) = -6 dan (-1) x 3 x 2 = -6

• Perkalian bilangan bulat juga bersifat asosiatif, artinya urutan pengelompokan bilangan yang dikalikan tidak mempengaruhi hasil perkalian.
  Contoh: (4 x 2) x (-1) = -8 dan 4 x (2 x (-1)) = -8

• Bilangan bulat satu (1) adalah elemen identitas untuk perkalian, yaitu perkalian bilangan bulat apa pun dengan satu akan menghasilkan bilangan bulat itu sendiri.
  Contoh: 5 x 1 = 5 dan (-8) x 1 = -8

• Bilangan bulat nol (0) adalah elemen nol untuk perkalian, yaitu perkalian bilangan bulat apa pun dengan nol akan menghasilkan nol.
  Contoh: 5 x 0 = 0 dan (-8) x 0 = 0

3. Operasi Pembagian bilangan bulat

Operasi pembagian bilangan bulat adalah proses untuk membagi dua bilangan bulat untuk mendapatkan hasil akhir. Operasi ini dapat dilakukan pada bilangan bulat positif, negatif, atau keduanya.

Namun, ada beberapa aturan yang perlu diperhatikan saat melakukan operasi pembagian bilangan bulat:

• Jika bilangan yang dibagi dan pembagi memiliki tanda yang sama (keduanya positif atau keduanya negatif), maka hasil pembagiannya akan positif.
  Contoh: 10 ÷ 2 = 5, (-12) ÷ (-4) = 3

• Jika bilangan yang dibagi dan pembagi memiliki tanda yang berbeda, maka hasil pembagiannya akan negatif.
  Contoh: 15 ÷ (-3) = -5, (-20) ÷ 4 = -5

• Pembagian oleh nol tidak didefinisikan dalam matematika, oleh karena itu tidak dapat dilakukan. Jadi, jika pembagi adalah nol, maka operasi pembagian tidak dapat dilakukan.
  Contoh: 12 ÷ 0 = Tidak didefinisikan

• Operasi pembagian tidak bersifat komutatif, artinya urutan bilangan yang dibagi dan pembagiannya mempengaruhi hasil pembagian.
  Contoh: 10 ÷ 5 = 2, tetapi 5 ÷ 10 = 0,5

• Operasi pembagian tidak bersifat asosiatif, artinya urutan pengelompokan bilangan yang dibagi dan pembagiannya mempengaruhi hasil pembagian.
  Contoh: (20 ÷ 5) ÷ 2 = 2 dan 20 ÷ (5 ÷ 2) = 8

4. Operasi Pengurangan Bilangan Bulat

Operasi pengurangan bilangan bulat adalah proses untuk mengurangi bilangan bulat satu dengan yang lain untuk mendapatkan hasil akhir. Operasi ini dapat dilakukan pada bilangan bulat positif, negatif, atau keduanya.

Untuk melakukan operasi pengurangan bilangan bulat, kita perlu mengetahui aturan-aturan berikut:

• Jika kedua bilangan memiliki tanda yang sama (keduanya positif atau keduanya negatif), maka kita dapat mengurangkan bilangan yang lebih kecil dari bilangan yang lebih besar, dan menjaga tanda mereka sebagai tanda hasilnya.
  Contoh: 7 – 3 = 4, (-9) – (-2) = -7

• Jika kedua bilangan memiliki tanda yang berbeda, maka kita dapat mengubah operasi pengurangan menjadi operasi penjumlahan dan menggunakan nilai absolut (nilai tanpa tanda) dari kedua bilangan untuk menentukan jumlahnya. Tanda hasilnya kemudian diambil dari bilangan dengan tanda yang lebih besar.
  Contoh: 8 – (-3) = 8 + 3 = 11, (-4) – 7 = -(4 + 7) = -11

• Pengurangan bilangan bulat juga bersifat komutatif, artinya urutan bilangan yang dikurangkan tidak mempengaruhi hasil pengurangan.
  Contoh: 6 – 3 = 3 dan 3 – 6 = -3

• Pengurangan bilangan bulat juga bersifat asosiatif, artinya urutan pengelompokan bilangan yang dikurangkan tidak mempengaruhi hasil pengurangan.
  Contoh: (9 – 5) – 2 = 2 dan 9 – (5 – 2) = 6

• Bilangan bulat nol (0) adalah elemen identitas untuk pengurangan, yaitu pengurangan bilangan bulat apa pun dengan nol akan menghasilkan bilangan bulat itu sendiri.
  Contoh: 7 – 0 = 7 dan (-5) – 0 = -5

Inilah Kumpulan Contoh Soal Latihan Materi Hitung Bilangan Bulat Paling Lengkap

Berikut adalah beberapa contoh soal yang berkaitan dengan bilangan bulat:

Contoh Soal 1.

Jumlah dari 3 bilangan bulat positif berturut-turut adalah 36. Bilangan tersebut adalah?

• Jawaban

Jika x, y, dan z masing-masing merupakan bilangan bulat positif, maka x + y + z = 36. Kita juga tahu bahwa bilangan tersebut berturut-turut, sehingga kita dapat menuliskannya sebagai x, x+1, dan x+2. Maka persamaan yang terbentuk adalah:

• x + (x+1) + (x+2) = 36
• 3x + 3 = 36
• 3x = 33
• x = 11

Maka, bilangan-bilangan tersebut adalah 11, 12, dan 13.

Contoh Soal 2.

Apa bilangan bulat terkecil yang dapat dibagi oleh 5, 6, dan 7 secara bersamaan?

• Jawaban

Untuk menyelesaikan masalah ini, kita dapat mencari bilangan bulat terkecil yang dapat dibagi oleh kelipatan dari 5, 6, dan 7. Kelipatan dari 5, 6, dan 7 adalah 30, 42, dan 35, masing-masing. Oleh karena itu, bilangan bulat terkecil yang dapat dibagi oleh 5, 6, dan 7 secara bersamaan adalah kelipatan dari ketiga bilangan tersebut, yaitu 210.

Contoh Soal 3.

Hitung nilai mutlak dari -8.

• Jawaban

Nilai mutlak dari sebuah bilangan bulat adalah jaraknya dari nol pada garis bilangan bulat. Oleh karena itu, nilai mutlak dari -8 adalah 8.

Contoh Soal 4.

Hitung hasil dari 5 x (7 – 3) + 2.

• Jawaban

Kita dapat menghitung ekspresi di dalam kurung terlebih dahulu, sehingga hasilnya adalah:

• 5 x (7 – 3) + 2 = 5 x 4 + 2 = 22.

Contoh Soal 5.

Berapakah bilangan bulat yang dapat membuat persamaan x + 7 = 13 menjadi benar?

• Jawaban

Untuk membuat persamaan menjadi benar, kita harus mencari bilangan yang jika ditambahkan dengan 7 akan menghasilkan 13. Oleh karena itu, bilangan tersebut adalah 6.

Contoh Soal 6.

Jika a = 5 dan b = 7, berapa hasil dari a + b dan a x b?

• Jawaban:

• a + b = 5 + 7 = 12
• a x b = 5 x 7 = 35

Contoh Soal 6

Jika x = 12 dan y = 4, tentukan nilai dari (x + y) x 2 – 3y

• Jawaban:
• (x + y) x 2 – 3y = (12 + 4) x 2 – 3(4) = 32

Contoh Soal 7.

Jika a = -6 dan b = 2, tentukan nilai dari |a| + |b|.

• Jawaban:
• |a| + |b| = |-6| + |2| = 6 + 2 = 8