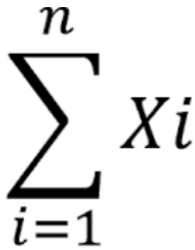Notasi Sigma – Setelah sebelumnya ContohSoal.co.id telah menerangkang materi tentang Rumus akar kuadrat Namun dipertemuan kali ini ContohSoal.co.id akan membahas materi tentang notasi sigma beserta pengertian, rumus sifat dan contoh soalnya. Untuk lebih lengkapnya sobat bisa simak ulasan yang sudah ContohSoal.co.id rangkum dibawah ini.
Pengertian Sigma
Sigma merupakan (huruf besar: Σ, huruf kecil: σ, huruf kecil pada akhir perkataan: ς) ialah huruf ke-18 dalam susunan alfabet Yunani.
Dalam sistem angka Yunani, huruf ini mempunyai nilai 200. Kemudian dalam bidang keilmuan, simbol huruf besar sigma, Σ digunakan sebagai lambang operator penjumlahan.
Pengertian Notasi Sigma
Pengertian Notasi Sigma ialah merupakansuatu simbol guna menjumlahkan beberapa bilangan terurut yang mengikuti suatu pola dan aturan tertentu.
Kemudian pada notasi sigma ialah masih mempunyai hubungan dengan materi barisan dan deret, baik aritmatika atau geometri. Dan dilambangkan dengan simbol = ∑.
Simbol tersebut merupakan sebuah Simbol Huruf yang berasal dari Yunani yang mempunyai arti sebagai Penjumlahan, dan perlu kalian ketahui juga bahwa Sejarah Notasi Sigma ini pertama kali memang digunakan oleh Bangsa Yunani sebagai salah satu Metode untuk menyederhanakan penjumlahan dari suatu barisan bilangan.
Materi Notasi Sigma
∑ merupakan notasi sigma, yang dapat digunakan untuk menyatakan penjumlahan berurutan dari suatu bilangan yang sudah berpola. Kemudian ∑ juga merupakan huruf capital “S” dalam abjad Yunani ialah huruf pertama dari kata SUM yang berarti jumlah.
Jika am , am+1 , am+2 , ….. an , merupakan bilangan real dan m dan n merupakan bilangan bulat sehingga menjadi m ≤ n, maka dapat dinyatakan :
∑n i =m α¹=am +am +¹am+² +….+αn
Dalam Notasi Fungsi, definis diatas tersebut dapat kita nyatakan antara lain :
∑n i=mf |i| = (m)+ f(m+1)+f(m+2)+….+f(n)
Jadi simbol ∑n i =mtersebut dapat menunjukkan penjumlahan dengan huruf i (dapat disebut indek penjumlahan) dan akan mengambil nilai bilangan bulat yang berurutan mulai dari m dan diakhiri dengan n.
Sifat – Sifat Notasi Sigma
Adapun sifat pada notasi sigma akan erat kaitanya dengan operasi penjumlahan pada bilangan. Simak berikut ini:
- Jika c konstanta, maka dinyatakan
| Sifat |
∑nf =1c=nc |
- Jika c konstanta, maka dinyatakan
| Sifat 2 |
∑nc a=cn∑a¹ |
- Jika c konstanta, maka dinyatakan
| Sifat 3 |
∑nf =1a1 +n∑b¹ |
- Jika 1<m<n, maka dapat dinyatakan sebagi berikut
| Sifat 4 | ∑ai n aif=1n ai¿∑nf =1f =1ai +n∑¿ i=mn ai |
- Jika m, n, p ialah konstanta , maka dapat dinyatakan
| Sifat 5 |
∑n¿k =m ∑n¿k =m |
Pembuktian :
Misalkan k = j – p, dengan k dan j merupakan variabel penjumlahan, maka :
a. f(k) = f( j – p).
b. Batas bawah penjumlahan akan berubah menjadi k = n ¿ > ¿ j – p = m ¿ > ¿ j = m + p.
c. Batas atas penjumlahan akan berubah menjadi k = n ¿ > ¿ j – p = n ¿ > ¿ j = n + p.
Rumus Notasi Sigma
| Rumus |
|
∑50 k²+∑50 k + ∑50 k=i12= 1/6 n(n+!)(n+2) + ¹/250(50 + 1 ) + (50 x 12)= 22.100 + 1.275 + 600= 23.975
2(1 ²+ 2² +3² + 4² + 5²) + 6 ( 1+2+3+4+5)=2(55) + 6(15)=200
Contoh Soal Notasi Sigma
Berikut ini akan kita bahas contoh soal dan penyelesaiannya :
Berapakah nilai notasi sigma berikut ini :∑4k=1 (3k² + 4k)
Penyelesaian :
∑4k=1 (3k² + 4k) = 3k² +∑4k=1 4k
Langkah berikutnya ialah oleh sebabnotasi sigma terdapat konstanta, maka kita dapat dijabarkan lagi sebagai berikut :
∑4k=1 3k² +∑4k=1 4k = 3 ∑4k=1k² + 4 ∑4k=1k
Kemudian , kerjakanlah penjumlahan sesuai dengan penjabaran, Yakni dengan mengganti k dengan batas penjumlahan, akan dimulai dari batas bawah = 1, dilanjutkan dengan 2, 3 dan terakhir ialah batas akhir = 4.
Jadi:
- 3 ∑4 k=1k² + 4 ∑4k=1 k
- = 3 (12 + 22 + 32 + 42) + 4 (1 + 2 + 32+ 4)
- = 3 (30) + 4 (10) = 310
Maka, nilai dari ∑4k=1k² (3k² +4k) ialah = 310
Demikianlah materi pembahasan kali ini mengenai notasi sigma, semoga artikel ini bermanfaat bagi sobat semua.
Artikel Lainnya: