Bangun ruang adalah objek tiga dimensi yang memiliki volume dan terdiri dari titik-titik, garis-garis, dan bidang-bidang. Bangun ruang dapat ditemukan di sekitar kita dalam berbagai bentuk dan ukuran, dan memainkan peran penting dalam matematika, fisika, arsitektur, dan berbagai bidang lainnya. Dalam artikel ini, kita akan menjelaskan pengertian, jenis-jenis, serta sifat-sifat penting yang terkait dengan bangun ruang.

Pengertian Bangun Ruang

Daftar Isi Tampilkan

Bangun ruang ialah merupakan sebuah penamaan atau sebutan untuk beberapa bangun-bangun yang berbentuk tiga dimensi atau bangun yang mempunyai ruang yang dibatasi oleh sisi-sisinya.

Ada sekitar 7 macam jenis bangun ruang, yakni : bangun ruang yaitu: kubus, balok, prisma, tabung, kerucut, limas dan bola.

7 Macam Jenis Bangun Ruang

Simak di bawah ini terdapat 7 macam jenis bangun ruang:

Bangun Kubus

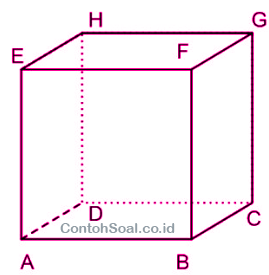
Kubus ialah sebuah bangun ruang yang memiliki panjang rusuk yang sama serta merupakan bangun yang di batasi oleh enam buah sisi yang sama dan sebangun, serta merupakan bangun ruang tiga dimensi.

Kubus ini memiliki 6 buah sisi, 12 buah rusuk dan 8 buah titik sudut.

Sifat – Sifat Kubus

Kubus memiliki beberapa sifat – sifat yang diantaranya yakni:

Memiliki6 sisi dengan bentuk persegi yang ukurannya sama luas
Mempunyai 12 rusuk yang ukurannya sama panjang
Mempunyai 8 titik sudut
Mempunyai 4 buah diagonal ruang
Mempunyai 12 buah bidang diagonal

Di bawah ini ialah gambarnya sebagai berikut:

Rumus Kubus

Luas salah satu sisi kubus

s²

Luas permukaan

6xs²

Volume

S³

Keliling

12xs

Keterangannya:
L= Luas permukaan kubus (cm²)
V= Volume kubus (cm³)
S= Panjang rusuk kubus (cm)

Bangun Balok

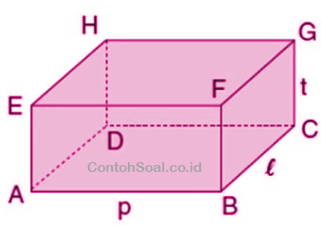
Balok ialah bangun ruang tiga dimensi yang dibentuk dari tiga pasang persegi atau persegi panjang, dengan setidaknya memiliki satu pasang di antaranya berukuran berbeda.

Sifat-Sifat Balok

Terdapat 4 sisi dengan membentuk persegi panjang (2 pasang persegi panjang yang ukurannya sama)
Mempunyai 2 sisi yang bentuknya sama (1 pasang persegi panjang dengan ukurannya sama namun berbeda ukuran dengan 2 pasang persegi panjang yang lain)
Mempunyai 12 rusuk yang ukurannya sama panjang
Mempunyai 8 buah titik sudut

Rumus – Rumus Balok

Permukaan

2x(pxl)+(pxt)+(lxt)

Diagonal

Akar dari(p kuadrat+l kuadrat+t kuadrat)

Keliling

4x(p+l+t)

Volume

pxlxt

Keterangannya :
P adalah Panjang (cm)
L adalah Lebar (cm)
T adalah Tinggi (cm)

Bangun Limas

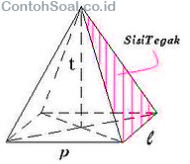
Limas ialah merupakan sebuah bangun ruang 3 dimensi yang memiliki alas yang berbentuk segi banyak dan bidang tegaknya berbentuk segitiga dan salah satu sudutnya bertemu di satu titik. Kawan bisa membacanya lebih lengkap pada artikel kami yang lain yakni rumus luas

Sifat – Sifat Limas

Bangun ruang limas ini memiliki beberapa sifat – sifat, diantaranya yaitu:

Mempunyai 5 sisi yaitu: 1 sisi berbentuk segiempat yang merupakan alas dan 4 sisi lainnya semuanya berbentuk segitiga serta merupakan sisi tegak.
Mempunyai 8 buah rusuk
Mempunyai 5 titik sudut yaitu: 4 sudut berada di bagian alas dan 1 sudut berada di bagian atas yang merupakan titik puncak.

Rumus Limas

Mencari Volume

1/3 x luas alas x tinggi sisi

Mencari Luas

luas alas+jumlah luas sisi tegak

Bangun Bola

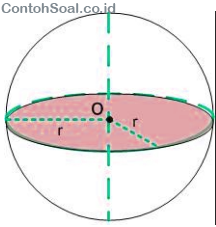
Bola ialah sebuah bangun ruang sisi lengkung yang dibatasi oleh satu bidang lengkung.

Sifat – Sifat Bola

Mempunyai alas berbentuk segienam
Mempunyai 6 sisi
Mempunyai 10 rusuk
Mempunyai 6 titik sudut

Rumus-Rumus Bola

mencari volume

4/3 x π x r³

mencari luas

4 x π x r²

V : Volume bola (cm³)
L : Luas permukaan bola (cm²)
R : Jari – jari bola (cm)
π : 22/7 atau 3,14

Bangun Kerucut

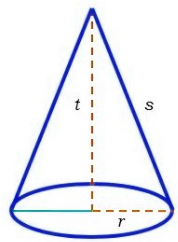
Kerucut ialah merupakan salah satu bangun ruang yang mempunyai sebuah alas yang berbentuk lingkaran dengan selimut yang memiliki irisan dari lingkaran.

Sifat-Sifat Kerucut

Ada beberapa sifat pada bangun ruang kerucut, diantaranya yaitu:

Mempunyai 2 sisi (1 sisi merupakan alas yang berbentuk lingkaran dan 1 sisinya lagi berupa sisi lengkung atau selimut kerucut)
Mempunyai 1 rusuk
Mempunyai 1 titik sudut

Rumus pada bangun ruang kerucut

Mencari volume

1/3xπxrxrxt

Mencari Luas

luas alas+luas selimut

Keterangan:

r = jari – jari (cm)
T = tinggi(cm)
π = 22/7 atau 3,14

Bangun Tabung

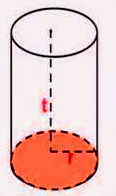
Bangun Tabung ialah merupakan sebuah bangun ruang tiga dimensi yang memiliki tutup dan alas yang berbentuk lsebuah ingkaran dengan ukuran yang sama dengan di selimuti oleh persegi panjang.

Sifat-Sifat Tabung

Terdapat beberapa sifat pada tabung, yaitu:

Memiliki3 sisi(yang 2 sisi berbentuk lingkaran dan 1 sisi berupa selimut tabung )
Mempunyai 2 rusuk

Rumus – Rumus pada Tabung

Rumus luas alas

luas lingkaran=π x r²

Rumus volume pada tabung

π x r² x t

Rumus keliling alas pada tabung

2 x π x r

Rumus luas pada selimut tabung

2 x π x r x t

Rumus luas permukaan tabung

2xluas alas+luas selimut tabung

Rumus kerucut + tabung

volume Luas

(π.r².t )+( 1/3.π.r².t ) (π.r²)+(2.π.r.t)+(π.r.s)

Rumus tabung + 1/2 bola

Rumus volume Rumus Luas

π.r².t+2/3. π.r³ (π.r²)+(2.π.r.t)+(½.4.n.r²) = (3.π.r²)+(2. π .r.t)

Rumus tabung+bola

Rumus Volume Rumus Luas

2 x π x r x t (2. π.r²)+(4. π.r²) = π.r²

Keterangannya:

V = Volume tabung(cm³)
π = 22/7 atau 3,14
r = Jari–jari/setengah diameter (cm)
t = Tinggi (cm)

Bangun Prisma

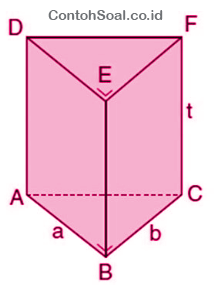
Prisma dapat didenisikan sebuah hasil dari gabungan antara bangun datar 2 dimensi baik dari bangun datar persegi panjang atau bangun datar segitiga.

Sifat – Sifat Prisma

Terdapat beberapa sifat pada prisma, diantaranya yaitu:

Mempunyai bidang alas dan bidang atas berupa segitiga yang kongruen (2 alas tersebut juga merupakan sisi prisma segitiga)
Mempunyai 5 sisi (2 sisi berupa alas atas dan bawah, 3 sisi lainnya merupakan sisi tegak yang semuanya berbentuk segitiga)
Mempunyai 9 rusuk
Mempunyai 6 titik sudut

Rumus-Prisma

Mencari Luas

(2xL. alas)+ (L. seluruh bidang tegak)

Volume Prisma

1/2 x a.s x t.s x t

Mecari Keliling

K = 3s (s + s + s)

Contoh Soal Bangun Ruang

Contoh Soal 1

Terdapat sebuah tabung berisi air dengan tinggi 18 cm, dimasuki sebuah bola besi. kemudian diketahui Jari-jari bola dan tabung sama yakni 12 cm. Jika π = 3,14, berapakah sisa air di dalam tabung sesudah bola dimasukan?Penyelesaian :

Diketahui :

t = 18 cm
r = 12 cm

π = 3,14

Dit : sisa air dalam tabung ?

Jawab :

Vtabung = luas alas × tinggi
Vtabung = πr²t
Vtabung = 3,14 × 12 × 12 × 18
Vtabung = 8138,88 cm³
Vbola = 4/3 πr³
Vbola = 4/3 × 3,14 × 12 × 12 × 12
Vbola = 7234,56 cm³

sisa air dalam tabung = Vtabung – Vbola

sisa air dalam tabung = 8138,88 – 7234,56 = 904,32 cm³

Contoh soal 2.

Berapakah luas permukaan bola yang memiliki diameter 28 cm ?Penyelesaian :

Diketahui:d=28→r= 14

Dit : luas permukaan bola?

Jawab :

luas permukaan bola = 4πr²
luas permukaan bola = 4 × 22/7 × 14 × 14
luas permukaan bola = 2464 cm

Contoh soal 3.

Terdapat sebuah bola yang tepat berada didalam tabung sehingga bola tersebut menyinggung setiap sisi tabung. Jika diketahui volume tabung 825 cm³, maka berapakah volume bola ?Penyelesaian :

Diket : vtab = 825

Dit : vbola?

Jawab :

Volume tabung : volume bola = 3 : 2

maka

Vbola = 2/3 × 825
Vbola = 550 cm³

Kesimpulan

Bangun ruang adalah objek tiga dimensi yang memiliki volume dan terdiri dari titik-titik, garis-garis, dan bidang-bidang. Berbagai jenis bangun ruang seperti kubus, balok, prisma, tabung, kerucut, dan bola memiliki sifat-sifat unik yang memengaruhi jumlah rusuk, titik sudut, bidang, volume, dan luas permukaan. Penerapan bangun ruang sangat penting dalam berbagai bidang, dari arsitektur hingga ilmu pengetahuan dan matematika.