Momen inersia adalah salah satu konsep fundamental dalam fisika yang memiliki peran penting dalam memahami gerakan rotasi suatu benda. Konsep ini memperhitungkan sebaran massa dari suatu benda terhadap sumbu rotasi, yang memengaruhi seberapa sulit atau mudah benda tersebut untuk berubah kecepatan rotasinya. Momen inersia juga dikenal sebagai inersia rotasional atau inertia rotasional.

Pentingnya momen inersia tidak hanya terbatas pada lingkup fisika teoretis, tetapi juga memiliki aplikasi yang luas dalam kehidupan sehari-hari dan berbagai bidang ilmu pengetahuan dan teknologi. Dalam fisika, konsep ini digunakan untuk menganalisis gerakan rotasi pada berbagai sistem, mulai dari benda kecil seperti bola atau lingkaran hingga sistem kompleks seperti roda kendaraan atau benda-benda dalam ruang angkasa.

Momen inersia juga memiliki implikasi dalam desain mesin dan alat. Dalam industri, pemahaman yang baik tentang momen inersia diperlukan untuk merancang sistem mekanis yang efisien dan stabil. Sebagai contoh, dalam desain kendaraan, pemahaman tentang momen inersia roda sangat penting untuk memastikan kelincahan dan stabilitas kendaraan saat bergerak.

Selain itu, momen inersia juga berperan dalam olahraga. Pada olahraga yang melibatkan gerakan rotasi, seperti renang, bersepeda, atau bahkan dalam permainan seperti bola basket atau tenis, pemahaman tentang momen inersia dapat membantu atlet dalam meningkatkan kinerja mereka.

Dalam artikel ini, kita akan menjelajahi konsep momen inersia secara lebih mendalam, meliputi rumus-rumus dasar, contoh penerapan dalam kehidupan sehari-hari, faktor-faktor yang memengaruhi, serta relevansinya dalam teknologi modern. Dengan pemahaman yang lebih baik tentang momen inersia, kita dapat menghargai betapa pentingnya konsep ini dalam memahami alam semesta dan aplikasinya dalam kehidupan sehari-hari.

Pengertian Momen Inersia

Daftar Isi Tampilkan

Inersia ialah kecenderungan suatu objek untuk menahan keadaannya atau bergerak. Dengan kata lain, itu bisa disebut inersia objek. Objek yang sulit untuk bergerak memiliki kelembaman besar. Misalnya, bumi selalu berputar sehingga bumi memiliki inersia rotasi. Dengan cara ini kita dapat memahami momen inersia, yang merupakan ukuran inersia suatu objek yang berputar pada sumbunya.

Dalam arti momen inersia, ada hubungan dengan hukum Newton I. Hukum Newton I menjelaskan benda yang selalu bergerak namun juga tetap diam. Ini menjadikan momen inersia juga disebut Hukum Newton 1 atau Hukum Inersia. Selain itu, ada beberapa faktor yang mempengaruhi inersia dalam suatu benda, termasuk bentuk rotasi, massa benda, dan posisi sumbu rotasi.

Contoh Penerapan Momen Inersia

Momen inersia adalah konsep penting dalam fisika yang memiliki banyak penerapan dalam kehidupan sehari-hari dan berbagai bidang teknologi. Konsep ini memperhitungkan sebaran massa dari suatu benda terhadap sumbu rotasi, yang memengaruhi respons benda terhadap gaya rotasi yang bekerja padanya. Berikut adalah beberapa contoh penerapan momen inersia dalam kehidupan sehari-hari:

Roda: Salah satu contoh penerapan momen inersia yang paling umum adalah pada roda. Roda memiliki momen inersia yang berbeda-beda tergantung pada distribusi massa dari cakramnya. Ketika sebuah mobil berbelok, momen inersia roda menyebabkan roda cenderung melanjutkan gerakan rotasinya ke arah yang sama, yang menghasilkan stabilitas dan keamanan dalam perjalanan.

Lingkaran: Konsep momen inersia juga dapat diterapkan pada lingkaran. Sebuah lingkaran memiliki momen inersia yang berbeda tergantung pada distribusi massa dari lingkaran tersebut. Misalnya, saat seorang pesepeda memutar pedal sepedanya, momen inersia dari roda dan pedalnya memengaruhi seberapa mudah atau sulit untuk meningkatkan kecepatan putaran.

Baling-baling: Pada baling-baling pesawat terbang, momen inersia sangat penting. Baling-baling harus dirancang sedemikian rupa sehingga momen inersianya mendukung stabilitas penerbangan pesawat. Momen inersia yang tepat akan membantu baling-baling tetap dalam posisi yang benar saat pesawat berputar.

Alat Olahraga: Dalam olahraga seperti angkat besi atau gimnastik, momen inersia juga berperan penting. Misalnya, saat seorang atlet angkat besi menggerakkan batang besi di atas kepalanya, momen inersia dari batang besi memengaruhi seberapa mudah atau sulitnya untuk memulai, menghentikan, atau mengubah arah gerakan batang tersebut.

Permainan: Konsep momen inersia juga dapat ditemui dalam berbagai permainan, seperti bola basket atau tenis. Misalnya, saat seorang pemain basket melempar bola ke arah keranjang, momen inersia dari bola memengaruhi jalannya bola dan seberapa jauh bola dapat terbang sebelum jatuh ke tanah.

Rumus Inersia

Rumus momen inersia adalah rumus matematis yang digunakan untuk menghitung momen inersia suatu benda terhadap sumbu rotasinya. Rumus ini berbeda-beda tergantung pada bentuk benda dan distribusi massa dari benda tersebut. Secara umum, rumus momen inersia dapat dinyatakan sebagai:

I = m × R²

Deskripsi rumus inersia di atas:

I = Inersia (kg.m²)
m = massa partikel (kg)
R = radius putar (m)

Rumus-rumus ini memberikan nilai momen inersia relatif terhadap sumbu rotasi yang melewati pusat massa benda. Dengan menggunakan rumus-rumus ini, kita dapat menghitung momen inersia suatu benda dengan lebih mudah dan cepat, serta memahami bagaimana distribusi massa dari benda tersebut memengaruhi momen inersianya.

Menghitung momen inersia apabila sumbu putarnya tidak berada pada pusat masa

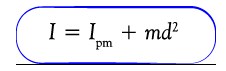
Inersia benda yang porosnya berada di pusat massa disebut inersia pusat massa. Jika sumbu rotasi tidak berada di pusat massa, persamaan berikut dapat digunakan untuk menentukan inersia.

Menghitung momen inersia jika benda berotasi

Jika objek berputar ialah objek kaku yang memiliki susunan massa kontinu, inersia dapat dihitung dengan metode integral.

Faktor-Faktor yang Mempengaruhi Momen Inersia

Faktor-faktor yang mempengaruhi momen inersia adalah variabel-variabel yang memengaruhi seberapa besar momen inersia suatu benda terhadap sumbu rotasinya. Beberapa faktor yang dapat memengaruhi momen inersia antara lain:

Bentuk Benda: Bentuk benda sangat mempengaruhi momen inersia. Benda yang memiliki bentuk tertentu akan memiliki distribusi massa yang berbeda-beda terhadap sumbu rotasi. Sebagai contoh, untuk benda dengan bentuk yang lebih merata seperti bola, momen inersianya akan berbeda dengan benda yang bentuknya lebih kompleks seperti tongkat atau piringan.
Jarak dari Sumbu Rotasi: Jarak antara titik massa benda dengan sumbu rotasi juga mempengaruhi momen inersia. Semakin jauh titik massa dari sumbu rotasi, semakin besar momen inersianya. Hal ini dapat dilihat dalam contoh sederhana seperti penggunaan tongkat. Saat tongkat diputar, titik massa yang lebih jauh dari ujung tongkat akan memiliki kontribusi yang lebih besar terhadap momen inersia.

Contoh Soal

Berikut ada beberapa contoh soal yang bisa membuat pembaca mempelajarinya.

Soal Pertama

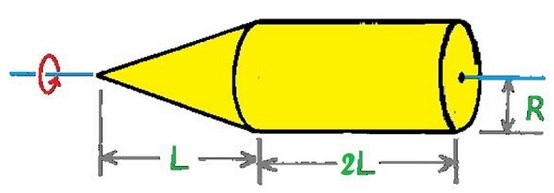
Terlihat gambar diatas. Maka diketahui massa dari silinder = massa kerucut yaitu sebesar 2kg, panjang silinder dari tersebut 0,8 m, dan jari-jari silinder 0,1 meter. Maka tentukanlah momen inersia dari pada gambar di atas.

Pembahasan:

Langkah pertama dalam penyederhanaan untuk menghitungnya, maka kita harus memisahkan perhitugan inersia tiap geometri benda.

I = I_{silinder} + I_{kerucut}

I = \frac{2}{3}m_sR_2^2 + \frac{3}{10} m_kR_k^2

Diketahui dari soal,

ms = 2 kg dan Rs = 0,1 m;
m2 = 2 kg dan Rk = 0,1 m;

Sehingga didapat besar inersia benda:

I = \frac{1}{2}(2)(0,1)^2 + \frac{3}{10}(2)(0,1^2)

I = 0,01 + \frac{3}{5}(0,01)

I = 0,01 + 0,006

I = 0,016 kg \cdot m^2

Soal Kedua

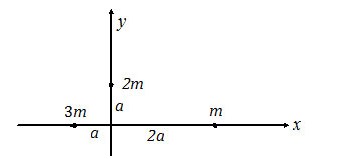
Pada akhir perancah, tiga partikel dengan massa m, 2 m dan 3 m dipasang, yang massanya diabaikan. Sistem ada di bidang xy. Ketika sistem diputar terhadap sumbu y, momen inersia sistem

Diskusi

Ketika sistem diputar tentang sumbu y, partikel dengan massa 2 m tidak akan berfungsi. Artinya, hanya partikel yang ada di sumbu x yang dihitung. Dengan asumsi bahwa partikel di sebelah kiri diindeks (1) dan partikel di sebelah kanan diindeks (2).
m1 = 3 m
m2 = m
R1 = a
R2 = 2a

Inersia dalam sistem adalah:
I = ΣmR2
= m1R12 + m2R22
= 3 m × a 2 + m × (2a) 2
= 3 m 2 + 4 m 2
= 7mA2
Inersia untuk sistem dengan demikian adalah 7 ma2 (E).