Mean, Median, Modus – Materi pembahasan kali ini mengenai contoh soal mean, median, modus, rumus dan jawabannya. Namun pada pertemuan sebelumnya kami juga telah membahas mengenai Trapesium Sama Kaki baiklah mari simak secara seksama ulasan di bawah ini.

Pengertian

Daftar Isi Tampilkan

Mean, median, dan modus antara data kelompok dan tunggal mempunyai nilai yang sama. Yang mana Nilai mean ialah merupakan rata – rata dari data yang diberikan. Kemudian Nilai median merupaan nilai tengah dari data yang telah diurutkan. Sedangkan modus ialah merupakan nilai yang paling sering muncul atau nilai dengan frekuensi paling tinggi. Untuk mendapatkan nilai mean, median, dan modus yakni seperti pada tabel di bawah.

Jenis	Rumus
Mean
Median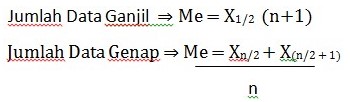
Modus	Nilai Yang Akan Sering Muncul

Keterangan Rumus :

X	Nilai Rata-Rata
	Jumlah dari seluruh Nilai Data
N	Jumlah dari seluruh Frekuensi

Penyajian Data kelompok Dalam Bentuk Tabel.

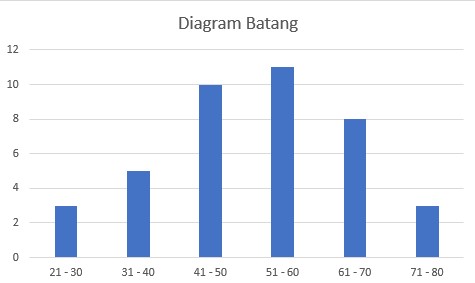
Nilai	Frekuensi
21 – 30	3
31 – 40	5
41 – 50	10
51 – 60	11
61 – 70	8
71 – 80	3

Bagi sobat semua yang ingin mencari berbagai materi terkait pembahasan mengenai matematika dan pembahasan yang bermanfaat lainnya, maka sobat semua dapat berkujung ke situs Dosenku.co.id Temukan berbagai materi terlangkap yang sudah kami sajikan disana.

Frekuensi	Banyaknya Data Yang Terdapat Pada Kelas Pertama
Tb	Batas Pada Bawa Kelas (51 – 0,5 = 50,5)
P	Panjang Kelas = 10 (21 – 30 = 21, 22, 23, 24, 25, 26, 27, 28, 29 dan 30 yaitu = 10 data) dan begitu seterusnya

Di dalam data kelompok berbentuk tabel memuat nilai batas bawah kelas, panjang kelas, dan nilai frekuensi dari kelas terkait.

Penyajian Data Dalam Bentuk Diagram Batang

Frekuensi	Banyaknya Data Yang Terdapat Pada Kelas Pertama yaitu = 3
Tb	Batas Pada Bawa Kelas (71 – 0,5 = 70,5)
P	Panjang Kelas = 10 (21 – 30 = 21, 22, 23, 24, 25, 26, 27, 28, 29 dan 30 yaitu = 10 data) dan begitu seterusnya

Rumus Mean (Rata-rata) Data Kelompok

Hasil untuk menentukan nilai rata-rata dari suatu data kelompok sama dengan mencari nilai rata-rata data tunggal. Idenya ialah menjumlahkan semua data kemudian membagi dengan banyaknyanya data. Namun oleh sebab penyajian pada data kelompok diberikan dalam bentuk yang berbeda, maka rumus mencari nilai mean untuk data kelompok sedikit berbeda dengan cara mencari nilai mean pada data tunggal.

Rumus mean data kelompok dinyatakan dalam persamaan di bawah ini:

Rumus Median Data Kelompok

Median ialah data tengah setelah diurutkan. Pada data tunggal, nilai median tersebut dapat dicari dengan mengurutkan datanya terlebih dahulu kemudian mencari data yang terletak tepat di tengahnya.cara ini hampir sama dengan cara mencari median . Karena bentuk penyajian datanya disajikan dalam bentuk kelompok,maka datanya tidak dapat diurutkan seperti pada data tunggal. Maka agar dapat mencari nilai median dari suatu data kelompok diperlukan sebuah rumus seperti berikut ini.

Rumus Modus Data Kelompok

Modus ialah nilai data yang paling sering muncul atau data yang memiliki nilai frekuensi paling tinggi.untuk mencari nilai modus pada data tunggal sangat mudah,yaitu dengan Cara mencari nilai data dengan frekuensi paling banyak.namun untuk mencari mencari nilai modus pada data kelompok tidak lah semudah kita mencari nilai modus pada data tunggal. Hal ini dikarenakan bentuk penyajian data kelompok yang disajikan dalam sebuah rentang kelas. Sehingga, nilai modus data kelompok tidak mudah untuk langsung didapatkan dan untuk menemukan nilai modus dari data kelompok maka kita perlu menggunakan sebuah rumus seperti dibawah ini.

Keterangan :

tb= tepi bawah kelas median
f1= selisih dari frekuensi kelas modus dengan frekuensi sebelum kelas modus
f2= selisih frekuensi pada kelas modus dengan frekuensi setelah kelas modus
p= panjang kelas interval

Contoh Soal dan Jawaban

Contoh Soal 1

Nilai rata-rata pada suatu ujian matematika dari 38 orang siswa yakni 51. Apabila nilai dari seorang siswa lain digabungkan pada kelompok tersebut maka berapakah nilai hitung ujian dari 39 siswa sekarang menjadi 52. Tentukanlah nilai yang diperoleh ..

Diketahui:

Nilai rataan hitung 38 siswa ialah 51. Nilai rataan hitung 39 siswa yakni 52.

Ditanyakan:

Pembahasan 1

Misalkan,

x_i = nilai ujian matematika dari siswa ke-i dengan i = 1, 2, …, 38

x₃₉ = nilai ujian matematika yang diperoleh Rahman

Dengan menggunakan rumus rataan hitung, berlaku :

Substitusikan persamaan (1) ke persamaan (2) diperoleh :

Maka, nilai ujian matematika yang diperoleh ialah 90.

Contoh Soal.2

Pada Tabel 3. diketahui menunjukkan hasil ulangan matematika dari 71 siswa Kelas XI SMA . Maka tentukan modus dari data tersebut.

Interval Kelas	Frekuensi
40 – 44	2
45 – 49	2
50 – 54	6
55 – 59	8
60 – 64	10
65 – 69	11
75 – 79	6
80 – 84	4
85 – 89	4
90 – 94	3

Jawaban.2

Diketahui bahwa kelas ke-7 mempunyai frekuensi terbesar (yakni 15) maka kelas ke-7 ialah merupakan kelas modus.

i = 44,5 – 39,5 = 5
L = Batas bawah nyata = 69,5 (tepi bawah kelas)
d₁ = 15 – 11 = 4
d₂ = 15 – 6 = 9

Maka ,tentukanlah nilai modus tersebut dengan menggunakan kalkulator. Apakah hasilnya akan sama?

3.2. Median dan Kuartil

Maka berdasarkan data kuantitatif yang tidak dikelompokkan dinyatakan pada x₁, x₂, …, x_n, (dengan x₁ < x₂ < … < x_n) untuk n yang berukuran besar yakni n ≥ 30) Jadi nilai dari ketiga kuartil itu ialah Q₁ (kuartil bawah), Q₂ (median), dan Q₃ (atas) ditentukan dengan rumus .

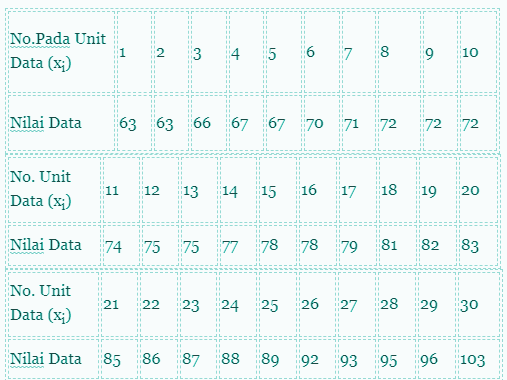
Contoh Soal.3

Tentukan median, kuartil Atas, dan bawah dari hasil data dibawah ini:.

67	86	77	92	75	70
63	79	89	72	83	74
75	103	81	95	72	63
66	78	88	87	85	67
72	96	78	93	82	71

Pembahasan.4

Urutkan data dari kecil ke besar hasilnya sebagai berikut.

dengan:L_i = batas bawah nyata dari kelas Q_iMaka pada data yang dikelompokkan terdapat nilai median (Me) dan kuartil (Q) yang ditentukan oleh rumus dibawah ini.

F_i = jumlah frekuensi kelass sebelum kelas kuartil ke-i
f_i = frekuensi kelas kuartil ke-i
n = banyak data
i = panjang kelas/interval kelas

Ingatlah :

Q₂= median
i pada F_idan f_iialah sebagai indeks. i yang berdiri sendiri sebagai panjang kelas.

Demikianlah Materi pembahasan kali ini mengenai contoh soal mean, semoga artikel ini dapat bermanfaat serta dapat menambah pengetahuan kita bersama.

Artikel ContohSoal.co.id Lainnya:

67	86	77	92	75	70
63	79	89	72	83	74
75	103	81	95	72	63
66	78	88	87	85	67
72	96	78	93	82	71

67	86	77	92	75	70
63	79	89	72	83	74
75	103	81	95	72	63
66	78	88	87	85	67
72	96	78	93	82	71

67	86	77	92	75	70
63	79	89	72	83	74
75	103	81	95	72	63
66	78	88	87	85	67
72	96	78	93	82	71