Contoh Soal Fungsi – Matematika merupakan pelajaran yang sangat menarik dan mengasyikan untuk dapat mengasah daya berpikii otak kita. Pada pelajaran matematika terdapat salah satunya pelajaran mengenai fungsi matematika. Nah, pada materi kali ini contohsoal akan membahas tentang contoh soal fungsi, sifat – sifat fungsi, jenis fungsi, rumus dan pembahasannya lengkap. Mari kita simak penjelasan lengkapnya berikut ini.
Pengertian Fungsi Matematika
Yang dimaksud fungsi dalam materi kali ini berbeda dengan pengertian fungsi pada umumnya. Adapun Fungsi matematika adalah sebuah relasi yang menghubungkan pada setiap anggota A pada suatu himpunan yang dapat disebut sebagai daerah asal atau (Domain) dengan suatu nilai tunggal f(x) dari sebuah anggota himpunan kedua yang disebut sebagai daerah kawan atau (Kodomain). Maka himpunan nilai yang didapat dari kedua relasi tersebut disebut sebagai daerah hasil atau (Range).
Terdapat istilah pada fungsi :
- Domain (daerah asal) fungsi f berlambang Df.
- Kodomain (daerah kawan) fungsi f berlambang Kf.
- Range (daerah hasil) disebut juga sebagai himpunan bagian dari kodomain. Range fungsi f berlambang Rf.
Nah, jika kita sudah sedikit paham dengan fungsi matematika. Selanjutnya mari kita bahas lebih dalam tentang pokok pembahasan fungsi yang mencakup jenis, sifat , contoh soal beserta pembahasannya.
Sifat – Sifat Fungsi Matematika
Adapun pada fungsi terdapat sifat – sifat fungsi matematika, diantaranya :
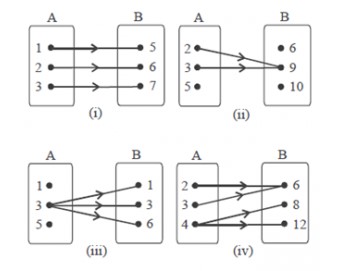
Fungsi Injektif (satu-satu)
Injektif atau sering disebut juga sebagai fungsi satu-satu. Secara artian harfiah kita belum bisa memahami secara luas. Maka, agar lebih mudah dalam pemahaman sifat fungsi injektif kita beri contoh, misalanya fungsi f menyatakan A ke B maka fungsi f dapat disebut sebuah fungsi injektif (satu-satu), jika pada setiap dua isi yang berlainan di himpunan A akan dipetakan pada dua isi yang berbeda di himpunan B. Maka secara singkat dapat dikatakan bahwa f:A→B adalah fungsi injektif jika a ≠ b maka f(a) ≠ f(b) atau ekuivalen, dan jika f(a) = f(b) maka a = b.
Fungsi Surjektif (into)
Sifat fungsi matematika berikutnya adalah surjektif atau onto.
Fungsi f: A → B dapatdisebut fungsi surjektif apabila pada setiap anggota himpunan B merupakan pasangan dari anggota himpunan A. Dengan kata lain, pada sebuah kodomain fungsi surjektif sama dengan kisarannya atau (range).
Fungsi Bijektif (Korespondensi satu-satu)
Sifat fungsi matematika berikut ini adalah yang terakhir yaitu Fungsi f: A→B Dapat disebut fungsi bijektif apabila fungsi f adalah fungsi injektif sekaligus juga fungsi surjektif. Maka dapat dikatakan f adalah fungsi yang bijektif atau A dan B berada dalam korespondensi satu-satu.
Contoh Fungsi Matematika :
Diketahui
A = {1, 2, 3, 4, 5}, B = {2, 3, 4, 5, 6}
C = {2, 4, 6, 8}
Tentukan sifat dari fungsi dalam bentuk himpunan pasangan berurutan di atas.
|
FUNGSI |
SIFAT |
|
Fungsi f: C -> A dengan f = {(2,1), (4,2), (6,4), (8,5)} |
Injektif |
| Fungsi f: A -> C dengan f = {(1,2), (2,4), (3,4), (4,6), (5,8)} |
Surjektif |
| Fungsi f: C -> B dengan f = {(2,2), (4,3), (6,3), (8,5)} |
Into |
|
Fungsi f: A -> B dengan f = {(1,2), (2,3), (3,4), (4,5), (5,6)} |
Bijektif |
Jenis – Jenis Fungsi Matematika
Secara umum, dapat dikatan fungsi terdiri dari fungsi aljabar dan juga fungsi transenden. Fungsi aljabar adalah sebuah fungsi yang didalam menggunakan bentuk aljabar. Sebaliknya fungsi yang tidak menggunakan bentuk dari aljabar disebut sebagai fungsi transenden.
Contoh fungsi aljabar
- fungsi konstan
- fungsi identitas
- fungsi linear
- fungsi kuadrat
- fungsi polinom
- fungsi modulus
- dll
Contoh fungsi eksponen
- fungsi logaritma
- fungsi trigonometri
- dll
Fungsi Linear
Jenis fungsi matematika pertama adalah fugsi linear yaitu Fungsi pada bilangan real didefinisikan f(x) = ax + b, a dan b konstan dengan a ≠ 0 disebut sebagai fungsi linear
Fungsi Konstan
Agar lebih mudah dipahami untuk jenis fungsi yang kedua ini, ada sedikit contoh mengenai fungsi konstan. Misalnya f:A→B adalah fungsi di dalam A maka fungsi f disebut fugsi konstan apabila dan hanya jika jangkauan dari f hanya terdiri dari satu anggota himpunan.
Fungsi Identitas
Jenis fungsi matematika selanjutnya adalah fungsi identitas. Contoh fungsi identitas f:A→B adalah fungsi dari A ke B maka f disebut sebagai fungsi identitas apabila dan hanya jika range f = kodomain atau di lambangkan dengan f(A)=B.
Fungsi Kuadrat
Sebuah Fungsi f: R→R yang ditentukan oleh rumus f(x) = ax2 + bx + c dengan a, b, c ∈ R dan a ≠ 0 disebut fungsi kuadrat.
Fungsi Polinom
Fungsi polinom merupakan bentuk umum dari beberapa fungsi konstan, fungsi identitas, fungsi linear, dan fungsi kuadrat.
Fungsi Irasional
Fungsi irasional merupakan fungsi yang berbentuk akar. Fungsi irasional didefinisikan jika bilangan di dalam akar tidak negatif atau (positif atau nol).
Fungsi Pecahan
Fungsi pecahan merupakan fungsi yang berbentuk pecahan dan terdefinisi apabila bilangan pada penyebut pecahan itu tidak sama dengan nol.
Fungsi Ganjil
Fungsi ganjil merupakan sebuah fungsi yang memenuhi f(-x) = -f(x). Dan grafiknya simetris kepada titik pusat O(0,0).
Fungsi Genap
Fungsi genap merupakan sebuah fungsi yang memenuhi f(-x) = f(x). Dan grafiknya simetris kepada sumbu Y.
Contoh Soal Fungsi Matematika dan Pembahasannya
Setelah kita telah mempelajari dengan lengkap pembahasan fungsi matematika dan sudah sedikit memahaminya, maka sekarang kita akan pelajari contoh soal fungsi matematika berikut ini :
Contoh Soal Fungsi A
Terdapat himpunan X, Y dan Z , manakah himpunan yang merupakan fungsi :
X = {(1, 1), (2, 3), (3, 5), (4, 7), (5, 8)}
Y ={(1, 6), (1, 7), (2, 8), (3, 9), (4, 10)}
Z ={(2, 5), (3, 6), (4, 7)}
Pembahasan :
Himpunan X dan Z merupakan suatu pemetaan atau fungsi. Adapun himpunan Y bukan termasuk fungsi, karena pada himpunan Y domain 1 muncul dua kali yaitu berelasi dengan 6 dan 7 pada
kodomain.
Contoh Soal Fungsi B
Diketahui :
f(x) = ax + b
f(-4 ) = -3
f(2) = 9
Tuliskan fungsi dan tentukan nilai a dan b.
Pembahasan :
f(x) = ax + b
f(-4 ) = a(-4) + b = -3
-4a + b = -3 —> x
f( 2 ) = a . 2 + b = 9
2a + b = 9 —> z
Eliminasikan x dan z dihasilkan :
-4a + b = -3
2a + b = 9 –
-6a = – 12
a = 2
substitusi nilai a = 2 pada 2a + b = 9
2.(2) + b = 9
4 + b = 9
b = 5
Maka diperoleh fungsi f(x) = 2x + 5
Contoh Soal Fungsi C
Diketahui :
A = {2, 3, 6}
B = {2, 4, 6, 8, 10, 11}
Berikan domain, kodomain, dan range pada relasi di atas :
pembahasan :
{2, 4, 6} –> domain
{2, 4, 6, 8, 10, 11} –> kodomain
{ 2, 4, 6, 8, 10} –> Range
Contoh Soal Fungsi D
Untuk menjawab pertanyaan berikut ini, maka perhatikan gambar di bawah ini :
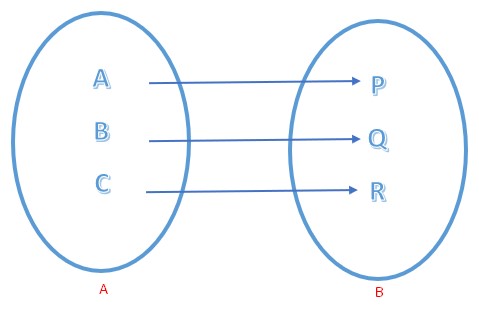
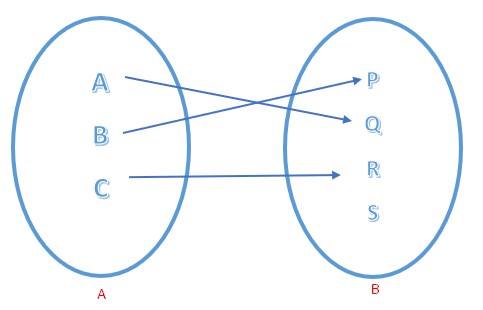
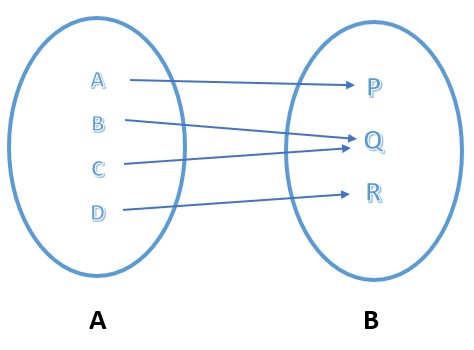
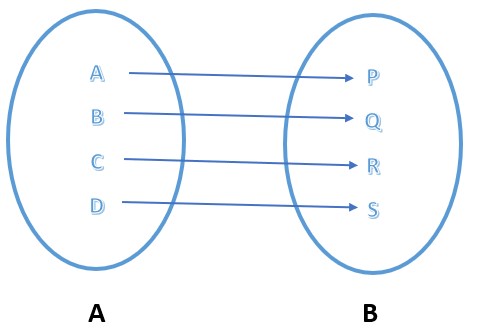
Dari himpunan di atas, manakah yang disebut himpunan fungsi dan berikan penjelasannya :
Pembahasan :
Sebelum kita dapat menjawab contoh soal di atas, maka terlebih dahulu harus kita pahami syarat suatu relasi untuk dapat dikatakan fungsi.
- Dikatakan fungsi apabila setiap anggota himpunan A memiliki satu pasangan terhadap anggota himpunan himpunan B
- Dikatakan bukan apabila ada salah satu anggota himpunan A tidak mempunyai pasangan kepada anggota himpunan B
- Dikatakan bukan sebuah fungsi apabila ada anggota himpunan A tidak mempunyai pasangan anggota B serta ada salah satu dari anggota himpunan A yang memiliki pasangan anggota himpunan B lebih dari satu
- Dikatakan bukan fungsi apabila satu dari anggota himpunan A memiliki lebih dari satu pasangan anggota himpunan B
Sekarang sudah dapat dibedakan antara yang fungsi dan bukan sebuah fungsi.
Contoh Soal Fungsi E
Diketahui :
Anggota Himpunan A = {2, 3, 4};
Anggota Himpunan B = {1, 2, 3, 4, 5, 6, 7};
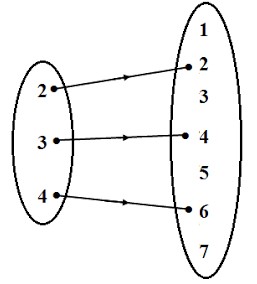
Fungsi f : A ->B ditentukan oleh f(x) = 2x – 2.
a. Tentukanlah range fungsi f.
b. Gambarlah fungsi f dengan diagram panah.
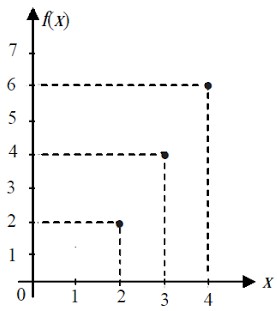
c. Gambarlah ke dalam diagram cartesius fungsi f.
Pembahasan :
a. Menggunakan fungsi f(x)= 2x – 2 maka:
- f(1) = 2 * 2 – 2 = 2
- f(2) = 2 * 3 – 2 = 4
- f(3) = 2 * 4 – 2 = 6
Maka, range fungsi f ialah {2, 4, 6}.
b. Di bawah ini gambar fungsi f diagram panah
c. Di bawah ini gambar fungsi f diagram Cartesius.
Contoh Soal Fungsi F
Tentukanlah domain atau (daerah asal) dan range fungsi f(x) = x2 + 3 jika x ∈ B dan B = {x | –3 < x ≤ 2}.
Pembahasan :
Adapun domain dari fungsi tersebut {–2, –1, 0, 1, 2}. Sedangkan range apat dicari dengan cara memasukan nilai domain ke fungsi f(x) = x2 + 3
f(–2) = (–2)2 + 3 = 7
f(–1) = (–1)2 + 3 = 4
f(0) = (0)2 + 3 = 3
f(1) = (1)2 + 3 = 4
f(2) = (2)2 + 3 = 7
Maka, range fungsi f(x) = x2 + 3 adalah {3, 4, 7}
Demikianlah materi Contoh Soal Fungsi, Sifat, Jenis, Rumus dan Pembahasannya Lengkap kali ini, semoga pelajaran ini dapat bermanfaat serta dapat menambah ilmu pengetahuan kita semua.
Lihat juga :