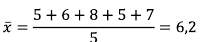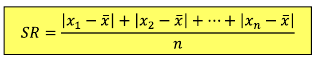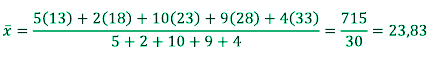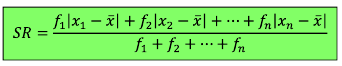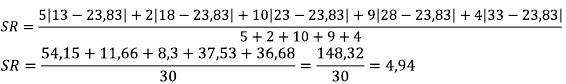Simpangan rata-rata adalah konsep statistik yang penting dalam menganalisis dan menggambarkan data. Saat mengumpulkan data, kita seringkali ingin mengetahui seberapa tersebar nilai-nilai tersebut dari nilai rata-rata. Dalam artikel ini, kita akan menjelaskan apa yang dimaksud dengan simpangan rata-rata, mengapa hal ini penting dalam statistik, dan bagaimana cara menghitungnya.
Pengertian Simpangan Rata-Rata
Simpangan rata-rata adalah ukuran yang digunakan untuk mengetahui sejauh mana nilai-nilai dalam suatu kumpulan data menyebar dari nilai rata-ratanya. Dalam pengertian sederhana, simpangan rata-rata adalah rata-rata dari selisih antara setiap nilai dalam kumpulan data dengan nilai rata-ratanya. Semakin tinggi simpangan rata-rata, semakin tersebar data tersebut dari nilai rata-rata.
Rumus Simpangan Rata-Rata
Sekumpulan data kuantitatif yang tidak dikelompokkan serta dinyatakan oleh x1, x2, …, xn. Dari data tersebut dapat ditentukanlah simpangan rata-rata (SR) dengan menggunakan sebuah rumus sebagai berikut:
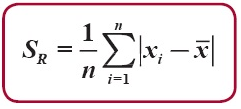
Rumus Variasi Dari Data Tunggal
Rumus variasi/ragam dari data tunggal ialah yang dinyatakan melalui persamaan di bawah ini:
Rumus Standar Deviasi/Simpangan Bakunya Data Tunggal
Rumus simpangan baku data tunggal dinyatakan melalui sebuah persamaan di bawah ini:
| Rumus Standar Deviasi | S = √S² = √ 1/n ∑¡=1(x¡- x¯)² |
| Keterangan |  = nilai data ke –i  = rata-rata n = jumlah seluruh frekuensi |
Simpangan Rata – Rata Data Berkelompok
Rumus (SR) Data Berkelompok
| Rumus Data kelompok | SR = 1/n ∑κ f¡=1|x¡- x¯ | |
| Keterangan | n = jumlah seluruh frekuensi  = frekuensi kelas ke-i = nilai tengah kelas ke-i = rata-rata k = banyaknya kelas interval |
Variasi (Ragam)
Persamaan untuk ragam atau variasi diberkan melalui rumus di bawah ini:
| Rumus Variasi/Ragam Data Kelompok | 1/n ∑¡=1(x¡- x¯)² / ∑κ i =1 fi |
| Keterangan | = nilai tengah kelas ke-i = frekuensi kelas ke-i = rata-rata k = banyak kelas interval |
Standar Deviasi (Simpangan Baku) Data Tunggal
Rumus simapangan baku untuk data kelompok ialah dibawah ini:
Rumus Simpangan Rata-Rata
Sekumpulan data kuantitatif yang tidak dikelompokkan serta dinyatakan oleh x1, x2, …, xn. Dari data tersebut dapat ditentukanlah (SR) dengan menggunakan sebuah rumus sebagai berikut:
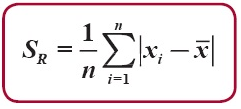
Contoh Soal Simpangan Rata-Rata
Bagi sobat semua yang ingin mencari berbagai materi terkait pembahasan mengenai matematika dan pembahasan yang bermanfaat lainnya, maka sobat semua dapat berkujung ke situs Quipper.co.id . Temukan berbagai materi terlangkap yang sudah kami sajikan disana.
Contoh Soal Simpangan Rata-Rata 1:
Hitunglah SR dari data kuantitatif berikut :12, 3, 11, 3, 4, 7, 5, 11
Pembahasan:
Maka, simpangan rata-ratanya ialah 3,25.
Pada suatu sekumpulan data bisa dinyatakan oleh x1, x2, …, xn kemudian masing-masing nilai data tersebut mempunyai frekuensi f1 , f2 , …, fn maka diperolehlah nilai simpangan rata-rata (SR) dengan menggunakan rumus.
Contoh Soal Simpangan Rata-Rata 2
Diberikan data sebagai berikut:
5, 6, 8, 5, 7Tentukan nilai SR data di atas!Pembahasan
Langkah awal terlebih dulu temukan rata-rata datanya:Setelah diketahui rata-ratanya, saatnya mencari SR:
Sehingga nilainya
- SR = | 5-6,2|+|6-6,2|+8 -6,2|+ |5 -6,2|+|7 -6,2| / 5
- SR = 1,2 +0,2 +1,8 +1,2 +0,8/5 = 5,2/5 =1,04
Contoh Soal Simpangan Rata-Rata 3
Perhatikan tabel distribusi frekuensi data dibawah ini
| Nilai | Frekuensi |
| 6 7 8 9 10 | 10 6 4 8 2 |
Tentukan nilaiSR data di atas!
Pembahasan
Agar dapat menemukan SR dari tabel distribusi frekuensi untuk data tunggal, maka terlebih dulu temukan rata-rata datanya:
x¯ = 10(6) + 6(7)+4(8)+8(9)=2(10) / 10 +6+4+8+2 =226/30= 7,53
Setelah diketahui rata-ratanya, saatnya mencari SR:
SR = f¹| x¹ -X¯|+….fn|Xn -X¯| / f¹ +f²+..+fn
Sehingga nilainya
Contoh Soal Simpangan Rata-Rata 4
Perhatikan tabel distribusi frekuensi data dibawah ini
| Nilai | Frekuensi |
| 11 – 15 16 – 20 21 – 25 26 – 30 31 – 35 | 2 2 10 9 4 |
Tentukan nilai SR data di atas!
Pembahasan
Temukan terlebih dulu titik tengah setiap kelas, untuk kemudian dicari reratanya:
| Nilai | Frekuensi | x |
| 11 – 15 16 – 20 21 – 25 26 – 30 31 – 35 | 2 2 10 9 4 | 13 18 23 28 33 |
Rata-ratanya ialah:
Dengan rumus yang sama soal sebelumnya saja,
tapi dipake titik tengah kelas sebagai x diperoleh:
Contoh Soal Simpangan Rata-Rata 5
Hitunglah SR dari data berikut ini!
4,5,6, 777 8, 8, 9, 9
Jawab:
Rata-ratanya ialah:= 7 SR
Contoh Soal Simpangan Rata-Rata 6
| xi | xi – | |
| 8 7 10 11 | -1 -2 1 2 | 1 2 1 2 |
Dari data di atas, diketahui rata-ratanya adalah 9. Carilah simpangan rata-ratanya.
Jawab :SR = = 1,5
Contoh Soal Simpangan Rata-Rata 7
Hitunglah SR nilai ulangan Matematika siswa Kelas XI MAN 2 Merdeka seperti Tabel 1 dibawah berikut:Tabel 1. Nilai ulangan Matematika siswa Kelas XI MAN 2 Merdeka
| Interval Kelas | Frekuensi |
| 40 – 44 | 3 |
| 45 – 49 | 4 |
| 50 – 54 | 6 |
| 55 – 59 | 8 |
| 60 – 64 | 10 |
| 65 – 69 | 11 |
| 70 – 74 | 15 |
| 75 – 79 | 6 |
| 80 – 84 | 4 |
| 85 – 89 | 2 |
| 90 – 94 | 2 |
Penyelesaian:
Dari tabel diatas, diperoleh = 65,7 (dibulatkan).
| KelasInterval | Nilai Tengah (xi) | fi | |x–x| | fi |x–x| |
| 40 – 44 | 42 | 3 | 23,7 | 71,1 |
| 45 – 49 | 47 | 4 | 18,7 | 74,8 |
| 50 – 54 | 52 | 6 | 13,7 | 82,2 |
| 55 – 59 | 57 | 8 | 8,7 | 69,6 |
| 60 – 64 | 62 | 10 | 3,7 | 37 |
| 65 – 69 | 67 | 11 | 1,3 | 14,3 |
| 70 – 74 | 72 | 15 | 6,3 | 94,5 |
| 75 – 79 | 77 | 6 | 11,3 | 67,8 |
| 80 – 84 | 82 | 4 | 16,3 | 65,2 |
| 85 – 89 | 87 | 2 | 21,3 | 42,6 |
| 90 – 94 | 92 | 2 | 26,3 | 52,6 |
| .Σfi = 71 | Σfi|x–x|=671,7 |
Maka, yang dapat dihasilkan dari simpangan rata-rata (SR) =671,7 / 71 = 9,46.
Perlu diingat:
Simpangan rataan hitung tersebut menunjukkan rataan hitung jauhnya datum dari rataan hitung.
Agar dapat menghitung simpangan baku dari data kuantitatif: 2, 5, 7, 4, 3, 11, 3 yakni bisa dengan menggunakan kalkulator ilmiah (fx–3600Pv) ialah sebagai berikut:
| 1) | Kalkulator “ON” | |
| 2) | MODE 3 → Program SD | |
| 3) | Masukkan data | |
| 2 data | ||
| 5 data | ||
| … | ||
| … | ||
| … | ||
| 3 data | ||
| 4) | Tekan tombol x αn-1 | |
| α = 2,878491669 = 2,88 |
Kesimpulan
Dalam kesimpulannya, simpangan rata-rata (SR) merupakan sebuah ukuran statistik yang penting dalam menganalisis keragaman data. Dengan menggunakan SR, kita dapat memahami sejauh mana nilai-nilai dalam suatu kumpulan data menyebar dari nilai rata-ratanya. Semakin tinggi nilai SR, semakin besar keragaman atau variasi data tersebut.
Penting untuk diingat bahwa simpangan rata-rata tidak memberikan gambaran tentang bentuk distribusi data, melainkan hanya tentang seberapa jauh nilai-nilai tersebut tersebar secara rata-rata dari nilai rata-ratanya.
Dalam aplikasinya, SR sering digunakan dalam berbagai bidang, termasuk ilmu sosial, ekonomi, ilmu alam, dan lain-lain. Misalnya, pengusaha dapat menggunakan SR untuk mengevaluasi konsistensi pendapatan harian dalam bisnis mereka. Semakin rendah nilai SR, semakin konsisten pendapatan harian toko atau bisnis tersebut.
Pengertian tentang simpangan rata-rata penting karena memberikan wawasan yang berarti dalam menginterpretasi data dan membuat keputusan berdasarkan analisis statistik yang akurat. Dengan memahami konsep ini, kita dapat mengoptimalkan penggunaan data dan meningkatkan pemahaman terhadap keragaman informasi yang kita miliki.
Dalam analisis statistik lebih lanjut, penting juga untuk mempertimbangkan faktor-faktor yang memengaruhi simpangan rata-rata, seperti variasi nilai dalam data, ukuran sampel, dan distribusi data. Dengan memahami faktor-faktor ini, kita dapat mengambil langkah-langkah yang tepat untuk mengurangi simpangan rata-rata jika diperlukan.
Penggunaan simpangan rata-rata dalam statistik deskriptif dapat dilengkapi dengan ukuran dispersi lainnya, seperti rentang, kuartil, dan varians, untuk memberikan gambaran yang lebih lengkap tentang data yang diamati.
Simpangan rata-rata adalah alat yang berguna dalam menganalisis data dan dapat memberikan pandangan yang lebih mendalam tentang keragaman dan konsistensi dalam berbagai situasi. Dengan memahami konsep ini, kita dapat mengambil keputusan yang lebih tepat dan informasi yang lebih berharga dalam berbagai aspek kehidupan.