Rumus ABC Dalam matematika, persamaan kuadrat adalah jenis persamaan yang paling umum dijumpai. Persamaan ini memiliki bentuk umum ax^2 + bx + c = 0, di mana a, b, dan c adalah konstanta, dan x adalah variabel. Untuk menyelesaikan persamaan kuadrat ini, kita menggunakan Rumus ABC, yang juga dikenal sebagai rumus kuadrat. Rumus ini sangat berguna dalam menemukan akar-akar persamaan kuadrat tersebut.
Pengertian Rumus ABC

Rumus ABC merupakan salah satu rumus yang dapat di gunakan untuk dapat mencari akar – akar persamaan kuadrat.
Rumus ABC di kenal dengan sebutan rumus kuadratis.
Ada beberapa syarat agar rumus ABC dapat di gunakan dan berlaku dalam sistem operasi matematika. Seperti dibawah ini :
- Persamaan kuadrat yang akan d ihitung memiliki bentuk ax2+bx c=0
- Dan A memiliki nila yaitu ≠0
Kemudian ada pula bilangan yang disebut dengan diskriminan, dimana bilangan berada pada posisi bagian bawah tanda akar yang terdapat pada rumus.
Bilangan diskriminan ini yang mana nilai D=b2−4ac. Dan rumus pada ABC dapat di terapkan serta dapat berlaku jika nilai D>0.
Jika ingin mendapat kan rumus ABC, kita bisa mengguna kan tiga cara dalam mengerjakan nya.
Pertama dengan dapat menggunakan pemecahan persamaan pada kuadrat, dengan cara melengkapi nilai – nilai terlebih dahulu melalui bentuk rumus dan kuadrat nya, kemudian kita juga dapat menggunakan cara pemfaktoran.
Formula faktor ABC atau biasa disebut sebagai rumus kuadrat ini juga biasa nya dapat digunakan dalam mencari operasi perhitungan yang mengarah pada persamaan kuadrat yang sulit di temukan secara umum.
Dan banyak orang yang sering menggunakan metode ini karena mudah dan simpel untuk dapat dimengerti.
Formula yang dipakai biasa disebut sebagai formula abc karena komponen yang ada di dalam nya hanya ada cara a,b,c dan tiap – tiap nya berupa konstanta, koefesien x, dan koefisien x2.
Kalkulator Rumus ABC
Formula ini berasal dari persamaan kuadrat secara umum yang dapat di pecahkan dengan cara melengkapi bentuk kuadrat yang sudah ada.
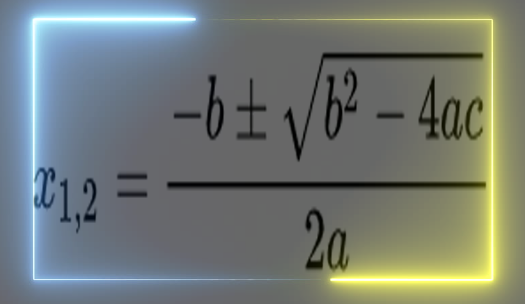
Rumus abc bisa dapat di gunakan dalam mencari akar – akar persamaan kuadrat yang dapat dipecah kan dengan cara melengkapi bentuk dari persamaan kuadrat. ax+by=c px+qy=d
Rumus ini dapat di gunakan untuk dalam menyelesaikan persamaan kuadrat dengan memiliki nilai koefisien a<1,a=1,a>1, dan di skriminan D>0, D=0, dan D<0.
Tetapi, jika berdasarkan dari pengalaman seputar dari kesalahan dalam memakai rumus abc dalam akar persamaan kuadrat, minus berada pada posisi di depan misalnya (-b±√…) dan terjadi kesalahan lagi yang sering dilakukan ialah hanya mensubsitusi nilai b tanpa mengartikan tanda minus.
Cara Mengerjakan Rumus ABC
Dalam mendapat kan rumus ABC ini, memiliki 3 cara yang dapat kita gunakan dalam mengerjakan nya.
Pertama kita harus terlebih dahulu dapat memecah kan persamaan kuadrat dengan mengguna kan pemfaktoran, maupun dengan cara melengkapi bentuk rumus dan kuadrat.
Namun pada pembahasan kali ini, kita akan membahas rumus ABC dengan lebih simpel sehingga kamu akan dapat memahami nya dengan lebih mudah.
Rumus ABC atau sering disebut dengan rumus kuadrat pada umum nya dapat digunakan untuk dapat menyelesaikan soal operasi persamaan kuadrat yang sulit untuk saling ditemukan.
Bahkan sebagian orang malah lebih mudah dengan menggunakan metode yang satu ini karena tanpa dasar pemfaktoran maupun mengisi faktor bentuk kuadrat.
Rumus ini biasa disebut dengan rumus ABC karena dalam komponen yang terdapat pada rumus ini hanya memakai cara a,b,c dan tiap – tiap nya berupa koefisien x2, konstanta, dan koefisien x.
Kelebihan Rumus ABC
- Dapat membantu kamu agar dapat berfikir secara rasional, sehingga logika tetap dapat di jalankan.
- Membantu kamu dalam melangkah dengan menggunakan sistematis, sesuai dengan langkah – langkah yang telah ada.
Maka dalam hal ini apabila sobat semua menggunakan rumus A b c dan dalam cara penerapan nya dalam berbagai persoalan, maka akan lebih untuk agar mempermudah cara berpikir kamu menjadi lebih rasional dan secara lebih sistematis.
Kenapa? Karena di dalam mengerjakan persoalan yang menggunakan rumus yaitu ABC, tentu akan membutuh kan usaha untuk kamu agar lebih mencermati nya dengan cara seksama.
Oleh karena itu, jika kamu sudah terbiasa dengan pemikiran yang seperti itu, akan lebih mudah utuk kamu agar dapat mendalami bagaimana logika yang tepat dalam menyelesaikan persoalan tersebut.
Kekurangan Rumus ABC
- Harus lebih cermat dan lebih teliti, jika tidak teliti maka kamu akan salah dalam pengerjaan soal.
Menjadi agar bisa lebih cermat dalam meneliti yang sebenar nya hal tersebut bukanlah sesuatu kekurangan untuk menerapkan rumus ABC, sebab hal ini sebenarnya merupakan suatu kekuatan.
Namun, dalam hal ini akan menjadi sesuatu kekurangan jika kamu merupakan tipe orang yang tidak teliti dan asal dalam mengerjakan.
Untuk itu dengan mnggunakan latihan mengerja kan berbagai macam latihan soal dengan menyelesaikan segala kasus rumus ABC, sehingga dapat menjadi sangat mudah untuk sobat dan juga proses belajar lebih cermat dalam upaya menyelesaikan soal.
Dalam hal ini sudah pasti saja akan menjadi suatu hal yang dapat berguna bagi kehidupan kamu dalam kehidupan sehari – hari, secara tidak sadar kamu akan di tuntut untuk berpikir agar dapat lebih teliti persoalan tersebut bisa kamu selesaikan dengan benar atau tidak ?
Dalam mengerjakan persoalan yang mengguna kan rumus ABC, kamu tidak haus dituntut dalam mengerja kan dengan cepat ketika baru pertama kali belajar.
Tetapi, kamu harus lebih dapat memahami bagaimana pola dalam pengerjaan yang benar agar jawaban yang di hasilkan dapat sesuai.
Contoh Soal Materi Rumus Persamaan Kuadrat ABC
Soal 1
Tentukan lah nilai akar persamaan kuadrat dari nilai abc=X2+7x+10=0
Yang nilai a adalah =1, b ialah=7, dan c ialah=10
Jawab:
- x1=-b+√b2 –√4ac:2a
- x1=-7+√72–4x1x10:2×1
- x1=-7+√49–√40:2
- x1=-7+3:2=-2
- x2=-b–√b2–√4ac:a
- x2=-7–√72–4 x1x10:2×1
- x2=-7–√49–√40:2
- x2=-7–3:2
- x2= -5
Jadi, nilai x adalah =-2 atau bisa juga nilai x ialah =-5
Soal 2
Hitunglah nilai himpunan penyelesaian dari= x2+2x=0
Jawab :
a=1, b=1, c=0
- x= -b + √b2 – √4ac : 2a
- x = -2 + √22 – 4 x 1 x 10 : 2 x 1
- x = -2 + √4 : 2
- x = -2 + 2 : 2
- x = -2 + 2 : 2
- x = 0 atau x = -2 – 2 : 2 = -2
Jadi, himpunan nya ialah ={-2,0}
Soal 3
Tentukan nilai himpunan soal dari x1,2 = -b + b2 – 4ac : 2a
Jawab :
- x2 – 2x – 3 = 0 -> a = 1, b = 2, c = -3
- x1,2 = – (-2) + √(-2)2 – 4 (1) (-3) : 2 x 1
- x1,2 = 2+ √16 : 2
- x1,2 = 2 + 4 : 2
- x1 = 2 + 4 : 2 = 6 : 2 = 3 atau x2 = 2 – 4 : 2 = -2 : 2 = -1
Jadi, nilai himpunan yang didapat adalah = {-1,3}
Soal 4
Carilah hasil dari persamaan kuadrat berikut ini apabila menggunakan rumus abc : x2 + 12x + 32 = 0
Jawab:
x2 + 12x + 32 = 0
a = 1
b = 12
c = 32
- x1,2 = -b + √b2 – √4ac : 2a
- x1,2 = -12 + √122 – 4 x 1 x 32 : 2 x 1
- x1,2 = -12 + √144 – √128 : 2
- x1,2 = -12 + √16 : 2
- x1,2 = -12 + 4 : 2
- x1,2 = -8 : 2
- x1 = -4
- x2 = -12 – 4
- x2 = -16 : 2
- x2 = -8
Maka, hasil dari persamaan kuadrat nya ialah = -4 dan -8
Soal 5
Hitunglah nilai x apabila : x2 – 2x – 3 = 0
Jawab:
a = 1, b = -2, c =-3
- x1,2 = -b + √b2 – √4ac : 2a
- x1,2 = – (-2) + √(-2)2 – √4 x 1 (- 3) : 2 x 1
- x1,2 = 2 + √4 + √12 : 2
- x1,2 = 2 + √16 : 2
- x1 = 2 + √16 : 2
- x1 = 2 + 4 : 2
- x1 = 6 : 2
- x1 = 3
- x2 = 2 – √16 : 2
- x2 = 2 – 4 : 2
- x2 = -2 : 2
- x2 = -1
Maka, himpunan yang didapatkan ialah = {3,-1}
Soal 6
Tentukan nilai dari 2x² + 4x – 6 = 0, A= 2, B= 4, C= -6
- x1,2=−b±b2–4ac√2a
x1,2=−4±42–4⋅2⋅(−6)√2⋅2
x1,2=−4±64√4
x1,2=−4±84
x1,2=−1±2 - x1=−1–2=−3
x2=−1+2=1
Maka, himpunan yang didapatkan adalah {-3, 1}.
Soal 7
Tentukan nila dari x² + 3x – 10 = 0, a = 1, b = 3, c = -10!
- x1,2=−b±b2–4ac√2a
x1,2=−3±32–4⋅1⋅(−10)√2⋅1
x1,2=−3±49√2
x1,2=−3±72 - x1=−3–72=−102=−5
x2=−3+72=42=2
Jadi, himpunan mempunyai nilai sama dengan {-5, 2}.
Soal 8
Dalam persamaan kuadrat diketahui nilai a = 1, b = 7, c = 10,
sehingga dapat disubstitusikan dengan menggunakan rumus ABC seperti di bawah ini :
- x = ( -b ± √b2 – 4ac )/ 2a
- x = ( -7 ± √72 – 4.1.(10) )/ 2.1
- x = ( -7 ± √49 + 40 )/ 2
- x = ( -7 ± √89 )/ 2
- x = (-7 + 3)/2
- x1 = (-7 – 3)/2 = -5
- x2 = (-7 + 3)/2 = -2
Sehingga bisa dikatakan bahwa nilai x1 = -5 dan x2 = -2.
Soal 9
Berapakah perkiraan nilai x jika persamaan kuadrat nya adalah x2 + 8x + 12 = 0?
Dalam persamaan kuadrat diketahui nilai a = 1, b = 8, c = 12,
sehingga dapat disubstitusikan kedalam rumus ABC sebagai berikut :
- x = ( -8 ± √b2 – 4ac )/ 2a
- x = ( -8 ± √82 – 4.1.(12) )/ 2.1
- x = ( -8 ± √64 – 48 )/ 2
- x = ( -8 ± √16 )/ 2
- x = (-8 + 4)/2
- x1 = (-8 – 4)/2 = -6
- x2 = (-8 + 4)/2 = -2
Sehingga bisa dikatakan bahwa nilai x = -6 dan -2.
Soal 10
Jika dalam persamaan kuadrat di ketahui : 2x2 – 5x – 3 = 0, maka berapa nilai x1 dan x2 ?
Jawab :
Diketahui dalam persamaan kuadrat nilai A =2, B = 5, C =-3,
sehingga bisa dapat disubstitusikan ke dalam rumus ABC seperti berikut:
- x = ( -b ± √b2 – 4ac )/ 2a
- x = ( -(-5) ± √(-5)2 – 4.2.(-3) )/ 2.2
- x = ( 25 ± √25 + 24 )/ 4
- x = ( 25 ± √49 )/ 4
- x = (5 + 7)/4
- x1 = (5 – 7)/4 = – 1/2
- x2 = (5 + 7)/4 = 3
Sehingga bisa dikatakan bahwa nilai x1 = -1/2 dan x2 = 3.
Soal 11
Jika diketahui dalam sebuah persamaan kuadrat ialah 2x2 – 5x – 3 = 0, tentukan berapa nilai x1 dan x2 ?
Jawab :
- x = ( -b ± √b2 – 4ac )/ 2a
- x = ( -(-5) ± √(-5)2 – 4.2.(-3) )/ 2.2
- x = ( 25 ± √25 + 24 )/ 4
- x = ( 25 ± √49 )/ 4
- x = (5 + 7)/4
- x1 = (5 – 7)/4 = – 1/2
- x2 = (5 + 7)/4 = 3
Sehingga dapat di katakan bahwa nilai x1 = -1/2 dan x2 = 3
Soal 12
Tentukan akar dari persamaan kuadrat dengan memakai penerapan rumus abc. x2+7x+10=0
Maka, nilai pada a ialah = 1,B=7,danC=10
Jawab :
X1 = -b + √b2 – √4ac : 2a
- = -7 + √72 – 4 x 1 x 10 : 2 x 1
- = -7 + √49 – √40 : 2
- = -7 + 3 : 2 = -2
X2= -b – √b2 – √4ac : 2a
- = -7 – √72 – 4 x 1 x 10 : 2 x 1
- = -7 – √49 – √40 : 2
- = -7 – 3 : 2
- = -5
Jadi, nilai pada x adalah =-2 atau bisa juga x ialah= -5
Dengan menggunakan Rumus ABC, kita dapat menyelesaikan berbagai masalah matematika yang melibatkan persamaan kuadrat dan mengaplikasikannya dalam berbagai bidang seperti fisika, ekonomi, dan rekayasa. Rumus ini merupakan salah satu konsep dasar yang penting dalam matematika yang membantu kita memahami pola dan hubungan antar variabel dalam persamaan kuadrat.
Berita Populer Lainnya:
