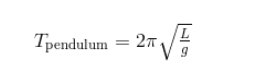Gerak Harmonik Sederhana – Pada kesempatan kali ini akan kembali kabarkan.com sampaikan materi pembahasan tentang Gerak Harmonik Sederhana dengan besertakan pengertian, teori, makalah dan contohnya. Namun diperjumpaan sebelumnya juga kabarkan.com telah menerangkan materi tentang Garis Vertikal, Horizontal, dan Diagonal Nah untuk lebih jelasnya langsung aja kita simak ulasannya di bawah ini.
Pengertian Gerak Harmonik Sederhana

Apa yang dimaksud dengan Gerak Harmonik Sederhana ? yakni merupakan suatu gerak secara bolak balik dengan teratur yang melalui sebuah titik yang mendikannya seimbang dengan berbagai getaran yang terjadi terhadap benda tersebut dalam setiap sekon selalu sama atau konstan.
Jika gerak yang terjadi secara berulang dalam selang waktu yang sama disebut gerak periodik.
Apabila gerak tersebut berlangsung dengan secara teratur maka hal tersebut dikenal juga dengan gerak harmonik.
Pada saat suatu partikel yang sedang bergerak secara periodik di sebuah lintasan yang sesuai atau serupa maka gerakan tersebut disebut juga dengan gerak osilasi/getaran.
Adapun secara sederhananya dari bentuk pada gerak periodik ialah sebuah benda yang berosilasi pada ujung pegas. Sehingga dengan hal tersebut kita mengenalnya dengan gerak harmonis sederhana.
Ketika sedang berlangsung suatu gerakan harmonik maka akan ada sejumlah besaran fisika yang ada pada benda terseut yakni:
- Pada Simpangan (y): merupakan sebuah jarak benda diawali dari titik pusat keseimbangan
- Pada Amplitudo (A): merupakan sebuah simpangan maksimum atau jarak terjauh
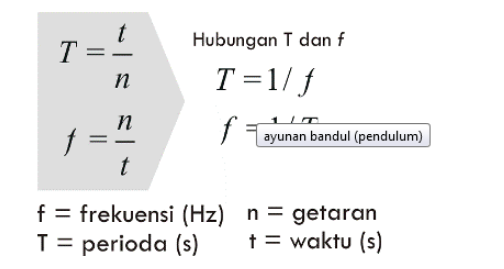
- Pada frekuensi (f): Yakni merupakan banyaknya getaran yang terjadi disetiap waktunya
- Pada Perioda (T): Yakni merupakan banyaknya waktu dalam satu getaran
Jenis Gerak Harmonik Sederhana
Di bawah ini terdapat 2 jenis gerak yang merupakan bagian dari Gerak Harmonik Sederhana yakni sebagai berikut:
- Yang pertama (GHS) Linier, yakni contohnya seperti alat penyedot dalam silinder gas, lalu gerak osilasi yang terjadi di air raksa, kemudian gerak horizontal atau juga secara vertikal dari pegas.
- Yang kedua (GHS) Angular, contohnya seperti gerak yang terjadi pada bandul/ fisis, atau juga pada osilasi ayunan torsi.
Kecepatan Untuk Berbagai Simpangan
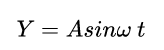
Pada Persamaan itu kemudian dikuadratkan
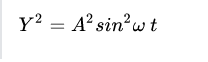
, maka akan diperoleh :
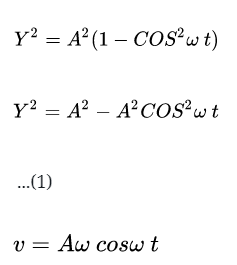
Kemudian atas persamaan tersebut:
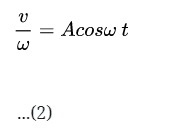
Jada atas Persamaan (1) dan (2) akan dikalikan, jadi yang diperoleh:
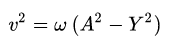
Keterangan:
- v = Merupakan kecepatan benda terhadap simpangan tertentu
- = Merupakan suatu kecepatan pada sudut
- A = Merupakan suatu amplitudo
- Y = Merupakan suatu simpangan
Percepatan Gerak Harmonik Sederhana
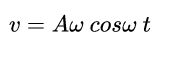
Atas persamaan kecepatan diatas: , jadi:

Pada percepatan maksimum apabila atau = 900 =
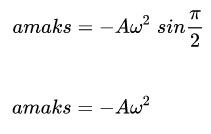
Keterangan:
- a maks = Merupakan suatu percepatan maksimum
- A = Merupakan suatu amplitudo
- = Merupakan suatu kecepatan sudut
Periode dan Frekuensi Getaran Harmonik
a. Periode dan Frekuensi Sistem Pegas
Secara umum, definisi atas gerak harmonik sendiri ialah merupakan suatu gerak secara melingkar dengan beraturan yang terjadi pada salah satu sumbu utama.
Maka oleh sebab itu, dalam T dan f yang terjadi pada pegas dapat dijumlahkan dengan cara menyesuaikan antara gaya pemulih(F=-kX) dan(F=-4π2mf2X).
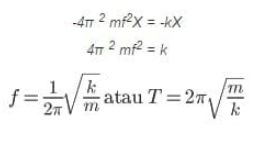
b. Periode dan Frekuensi Bandul Sederhana
- Gerak Harmonik Pada Bandul
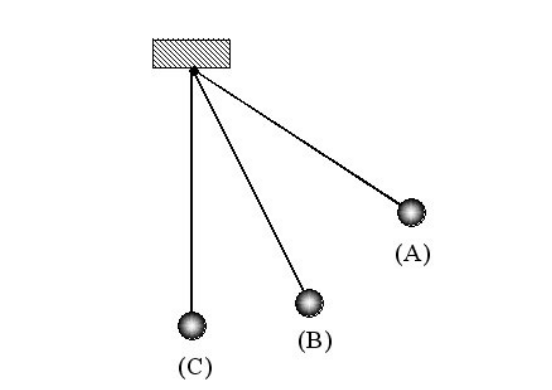
Persamaan:
Untuk ayunan bandul, dimana pada periode ayunan sangat tergantung pada ukuran panjang pada tali dan gravitasinya.
Maka apabila semakin besar dan panjang tali tersebut maka akan semakin panjang pula periodanya. Misalnya pada persamaan di bawah ini:
Keterangan:
T = Merupakan Perioda (s)
l = Merupkan suatu Panjang tali (m)
g = Merupakan suatu percepatan gravitasi (m/s2)
Dan biasanya pada Bandul sederhana atau pegas ini kerap digunakan guna mencari sebuah nilai percepatan gravitasi bumi dalam praktikum.
Contoh Soal Gerak Harmonik Sederhana
Terdapat sebuah benda yang bergerak sehingga menjadikan suatu gerakan harmonis dengan sebuah persamaan
y = 0,04 sin 20π t
Untuk y ialah merupakan suatu simpangan dalam satuan meter, t yakni waktu dalam satuan sekon.
Maka hitunglah beberapakah besaran atas persamaan getaran harmonis itu:
- a) amplitudo
- b) frekuensi
- c) periode
- d) simpangan maksimum
- e) simpangan saat t = 1/60 sekon
- f) simpangan saat sudut fasenya 45°
- g) sudut fase saat simpangannya 0,02 meter
Pembahasan
Maka dari pola persamaan pada simpangan gerak harmonik yang terdapat diatas yakni
y =A sin ωt
ω =2π f
atau
ω = 2π/T
- a) amplitudo atau A
y = 0,04 sin 20π t
A = 0,04 meter
- b) frekuensi atau f
y = 0,04 sin 20π t
↓
ω = 20π
2πf = 20π
f = 10 Hz
- c) periode atau T
T = 1/f
T = 1/10 = 0,1 s
- d) Pada simpangan maksimum /ymaks
y = A sin ωt
y = ymaks sin ωt
y = 0,04 sin 20π t
↓
y = ymaks sin ωt
ymaks = 0,04 m
(Simpangan maksimum tidak lain ialah amplitudo)
- e) Pada simpangan t = 1/60 sekon
y = 0,04 sin 20π t
y = 0,04 sin 20π (1/60)
y = 0,04 sin 1/3 π
y = 0,04 sin 60° = 0,04 × 1/2√3 = 0,02 √3 m
- f) Pada mulanya simpangan ketika sudut fasenya 45°
y = A sin ωt
y = A sin θ
dimana θ ialah merupakan sebuah sudut fase, θ = ωt
y = 0,04 sin θ
y = 0,04 sin 45° = 0,04 (0,5√2) = 0,02√2 m
- g) Maka pada sudut fase saat simpangannya 0,02 meter
y = 0,04 sin 20π t
y = 0,04 sin θ
0,02 = 0,04 sin θ
sin θ = 1/2
θ = 30°
Demikianlah materi pembahasan mengenai Gerak Harmonik Sederhana kali ini, semoga artikel ini dapat bermanfaat bagi sobat semua.
Artikel Lainnya :